PPO算法原理
参考:
- https://www.jianshu.com/p/9f113adc0c50
- https://zhuanlan.zhihu.com/p/468828804
- https://www.bilibili.com/video/av24724071/?p=4
PG（Policy Gradient）算法
强化学习中，有一个Agent作为我们的智能体，它根据策略\(\pi\)在不同的环境状态\(s\)下选择相应的动作来执行，环境根据Agent的动作，反馈新的状态以及奖励，Agent又根据新的状态选择新的动作，这样不断循环，直到游戏结束，便完成了eposide。在深度强化学习中，策略\(\pi\)是由神经网络构成，神经网络参数为\(\theta\)，表示成\(\pi_{\theta}\)。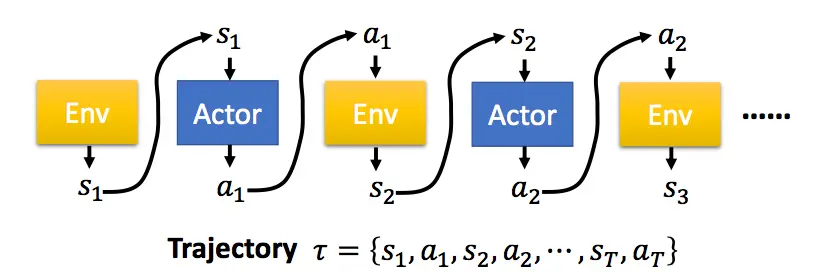 
一个完整的eposide序列，用\(\tau\)表示。而一个特定的\(\tau\)序列发生的概率为： \[
\begin{align}
p_{\theta}(\tau) \\
& =p(s_1)p_{\theta}(a_1|s_1)p(s_2|s_1,a_1)p_{\theta}(a_2|s_2)p(s_3|s_2,a_2)... \\
& =p(s_1)\prod_{t=1}^Tp_{\theta}(a_t|s_t)p(s_{t+1}|s_t,a_t)
\end{align}
\]
如果是固定的开局方式，上式中的\(p(s_1)\)可以省略掉。
对于一个完整的\(\tau\)序列，其在整个游戏期间获得的总奖励用\(R(\tau)\)表示。对于给定参数\(\theta\)的策略，其奖励期望为： \[\bar{R}_{\theta}=\sum_{\tau}R(\tau)p_{\theta}(\tau)=E_{\tau \sim p_{\theta}(\tau)}[R(\tau)]\]
对于一个游戏，我们自然希望通过调整策略参数\(\theta\)，得到的\(\bar{R}_{\theta}\)越大越好。所以就可以使用下面梯度下降的方式来求解，将\(\bar{R}_{\theta}\)对\(\theta\)求导： 
上面的过程中，我们首先利用log函数求导的特点进行转化，随后用N次采样的平均值来近似期望，最后将\(p_{\theta}\)展开，将与\(\theta\)无关的项去掉，即得到了最终的结果。
形象的解释上面的式子：每一条采样到的数据序列都希望\(\theta\)向着自己的方向进行更新。而在总体上，我们希望\(\theta\)向着奖励比较大的那条序列，因此用每条序列的奖励来加权平均他们的更新方向。
假设第三条数据的奖励很大，通过上述式子的更新策略，使得\(p_{\theta}(a_t^3|s_t^3)\)发生的概率更大，以后再遇到\(s_t^3\)这个状态的时候，我们就更倾向于采取\(a_t^3\)这个动作。
所以，一个PG方法的完整过程如下：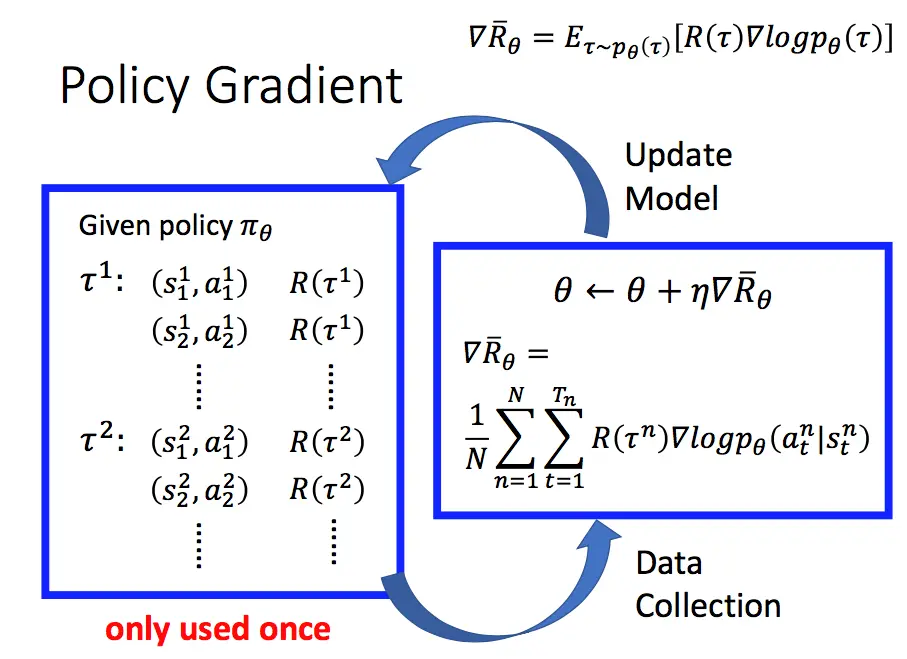 
我们首先采集数据，然后基于前面得到的梯度更新公式更新参数，随后再根据更新后的策略再次采集数据，再更新参数，如此循环进行。注意到图中only used once，因为在更新参数后，我们的策略已经变了，而先前的数据是基于更新前的策略得到的。
增加一个基线
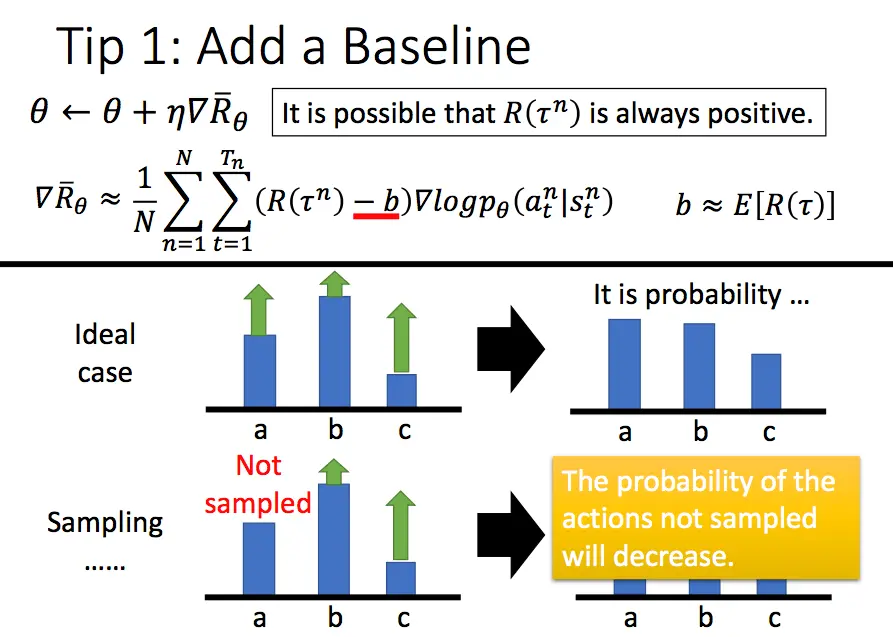
通过上面的介绍可以发现，PG方法在更新策略时，基本思想就是增加reward大的动作出现的概率，减小reward小的策略出现的概率。假设现在有一种情况，我们的reward无论何时都是正的，对于没有采样到的动作，它的reward是0.因此，如果一个比较好的动作没有被采样到，而采样到的不好的动作得到了一个比较小的正reward，那么没有被采样到的好动作的出现概率会越来越小，这显然是不合适的。因此我们需要增加一个奖励的基线，让reward有正有负。一般增加的基线是所获得奖励的平均值。 
增加折扣因子
类似买股票，未来1块钱的价值要小于当前1块钱的价值，因此未来1块钱变成现在的价值，需要进行一定的折扣。 
使用优势函数
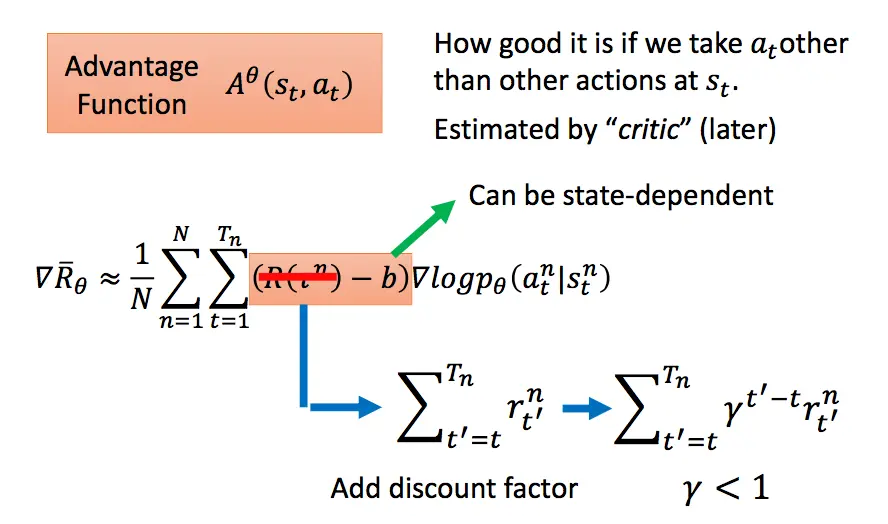
我们之前介绍的PG方法，对于同一个eposide中的所有数据，使用的奖励都是一样的。这样的做法不够细致，可以将奖励替换成关于\(s_t,a_t\)的函数，我们把这个函数叫做优势函数: \[A^{\theta}(s_t, a_t)=Q_{\pi}(s_t,a_t)-V_{\pi}(s_t)=\sum_{t'>t}\gamma^{t'-t}r_{t'}-V_{\phi}(s_t)\] 其中前半部分表示实际的折扣奖励，后半部分\(V_{\phi}(s_t)\)是拟合的折扣奖励，通过critic来计算得到，它由一个结构与策略网络相同但参数不同的神经网络构成，主要是来拟合从\(s_t\)到终局的折扣奖励。
\(A^{\theta}(s_t, a_t)\)表示在\(s_t\)状态下采用动作\(a_t\)时，实际得到的折扣奖励相对于模拟折扣奖励的优势。模拟的折扣奖励是在\(s_t\)状态下所有采样过动作的折扣奖励的拟合（通过critic模型拟合），因此优势函数代表了采用动作\(a_t\)相对于这些动作的平均优势。
PPO算法
接着上面的讲，PG方法一个很大的缺点就是参数更新慢，因为我们每更新一次参数都需要进行重新采样，这其实是on-policy的策略，即我们想要训练的agent和与环境进行交互的agent是同一个agent。与之对应的是off-policy策略，即想要训练的agent和与环境交互的agent不是同一个agent。
那么为了提升我们的训练速度，让采样到的数据可以重复使用，我们可以将on-policy的方式转换为off-policy的方式。即我们训练的模型是一个actor，与环境交互采样数据的模型使用另一个actor。 
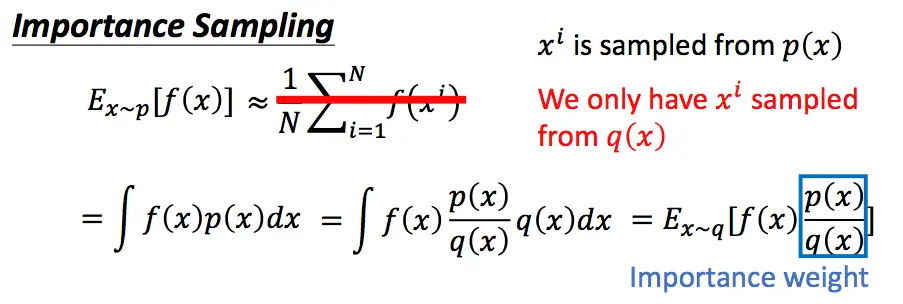通过这种方式，我们的\(p(x)\)和\(q(x)\)的分布不能差别太大。
那么此时我们想要期望奖励最大化，则变为： 
最后一项因为假设两个分布不能差太远，所以认为它们是相等的，为了求解方便，直接划掉。此时似然函数变为： \[J^{\theta'}(\theta)=E_{(s_t,a_t)\sim\pi_{\theta'}}\bigg[\frac{p_{\theta}(a_t|s_t)}{p_{\theta'}(a_t|s_t)}A^{\theta'}(s_t,a_t)\bigg]\]
前面介绍了，我们希望\(\theta\)和\(\theta'\)不要差太远。我们可以用KL散度来计算，将其加入PPO模型的似然函数中，变为： 
在实际中，我们会动态改变对\(\theta\)和\(\theta'\)分布差异的惩罚，如果KL散度太大，则增加这一部分的惩罚；如果小到一定的值，就减小这一部分的惩罚。基于此，我们得到了PPO算法的过程： 
PPO算法还有另一种实现方式，不将KL散度直接放入似然函数中，而是进行一定程度的裁剪： 
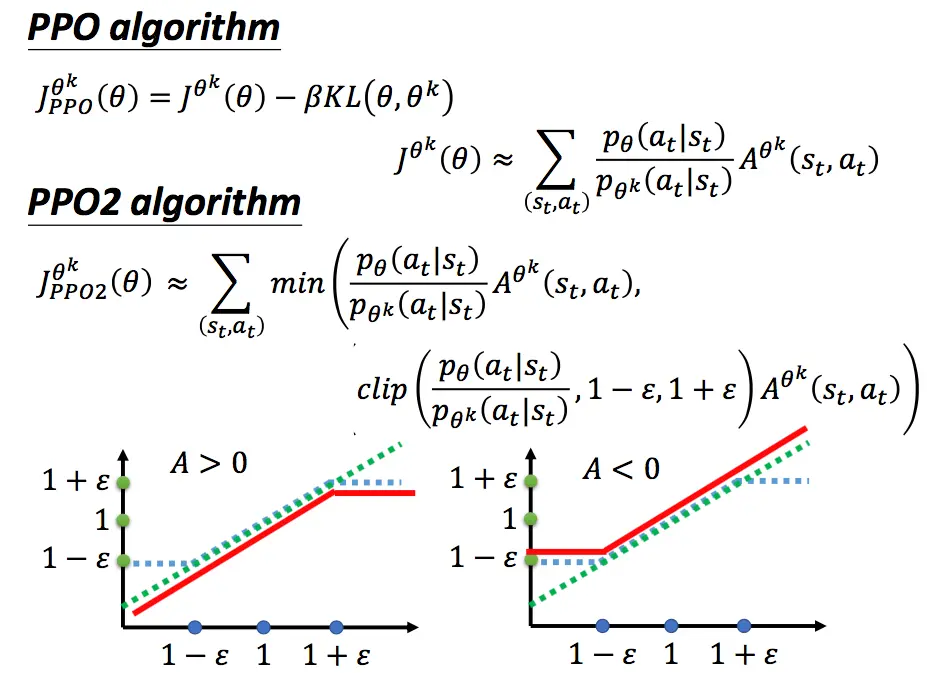上图中，绿色的线代表min中的第一项，即不做任何处理。蓝色的线为第二项，如果两个分布差距太大，则进行一定程度的裁剪。最后这两项取min，防止\(\theta\)更新太快。
通过上述介绍，我们可以看到PPO有四个网络参数：
- \(\theta\)：训练网络，每次都会被更新。(也就是大家说的actor模型)
- \(\theta'\)：训练网络副本，负责与环境交互采样数据。（也就是大家说的ref模型）
- \(\phi\)：奖励模型，拟合折扣奖励。（也就是大家说的critic模型，获取每个位置的奖励）
- \(reward model\): 奖励模型，获取一整句话的奖励。
PPO共涉及actor model，ref_model，reward model和critic model这四个模型，其实更新参数的模型只有actor model和critic model。
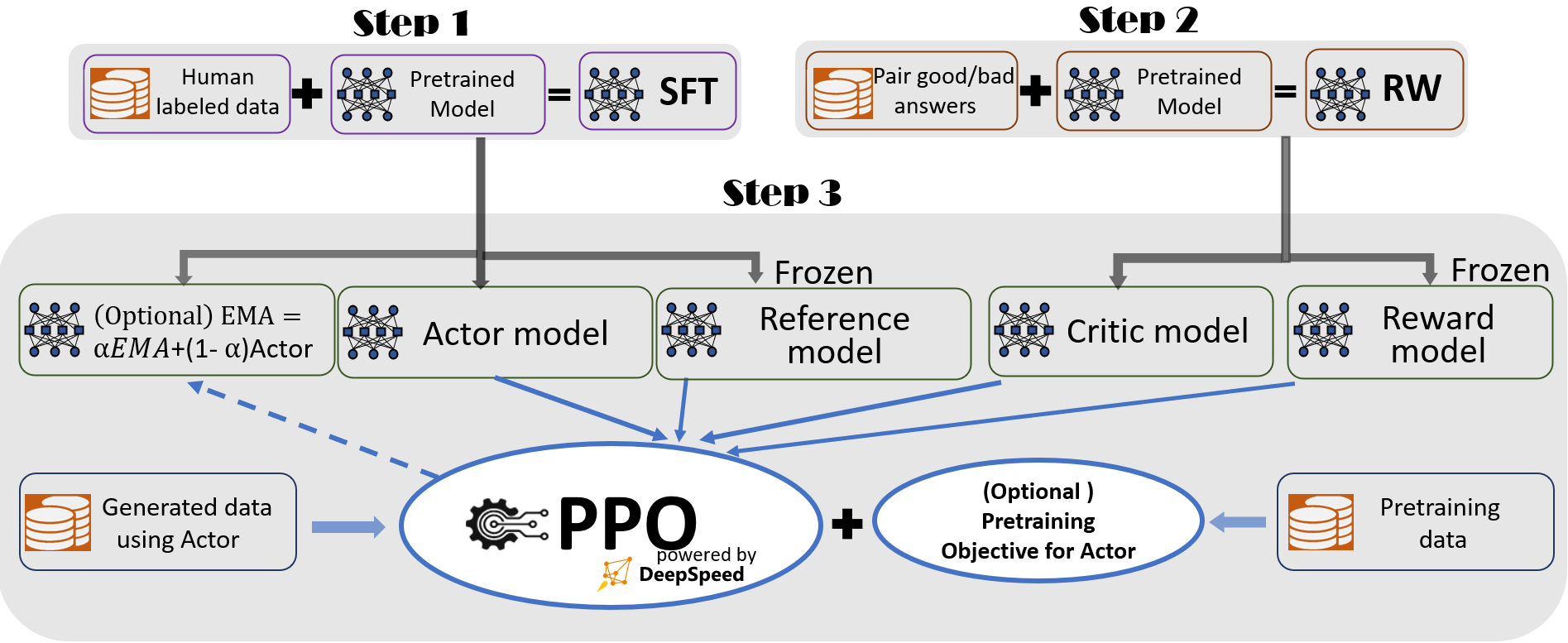
打个比喻来说，PPO的思路是： 0点时，我与环境进行互动，收集了很多数据。然后利用数据更新我的策略，此时我成为1点的我。当我被更新后，理论上，1点的我再次与环境互动，收集数据，然后把我更新到2点，然后这样往复迭代。
但是如果我仍然想继续0点的我收集的数据来进行更新。因为这些数据是0点的我（而不是1点的我）所收集的。所以，我要对这些数据做一些重要性重采样，让这些数据看起来像是1点的我所收集的。当然这里仅仅是看起来像而已，所以我们要对这个“不像”的程度加以更新时的惩罚（KL）。
其中，更新的方式是：我收集到的每个数据序列，对序列中每个（s, a）的优势程度做评估，评估越好的动作，将来就又在s状态时，让a出现的概率加大。这里评估优势程度的方法，可以用数据后面的总折扣奖励来表示。另外，考虑引入基线的Tip，我们就又引入一个评价者小明，让他跟我们一起学习，他只学习每个状态的期望折扣奖励的平均期望。这样，我们评估（s, a）时，我们就可以吧小明对 s 的评估结果就是 s 状态后续能获得的折扣期望，也就是我们的基线。注意哈：优势函数中，前一半是实际数据中的折扣期望，后一半是估计的折扣期望（小明心中认为s应该得到的分数，即小明对s的期望奖励），如果你选取的动作得到的实际奖励比这个小明心中的奖励高，那小明为你打正分，认为可以提高这个动作的出现概率；如果选取的动作的实际得到的奖励比小明心中的期望还低，那小明为这个动作打负分，你应该减小这个动作的出现概率。这样，小明就成为了一个评判官。
当然，作为评判官，小明自身也要提高自己的知识文化水平，也要在数据中不断的学习打分技巧，这就是对\(\phi\)的更新了。