VAE介绍
转载自https://spaces.ac.cn/archives/5253。
分布变换
通常我们会拿VAE跟GAN比较,的确,它们两个的目标基本是一致的——希望构建一个从隐变量\(Z\)生成目标数据\(X\)的模型,但是实现上有所不同。更准确地讲,它们是假设了\(Z\)服从某些常见的分布(比如正态分布或均匀分布),然后希望训练一个模型\(X=g(z)\),这个模型能够将原来的概率分布映射到训练集的概率分布,也就是说,它们的目的都是进行分布之间的变换。
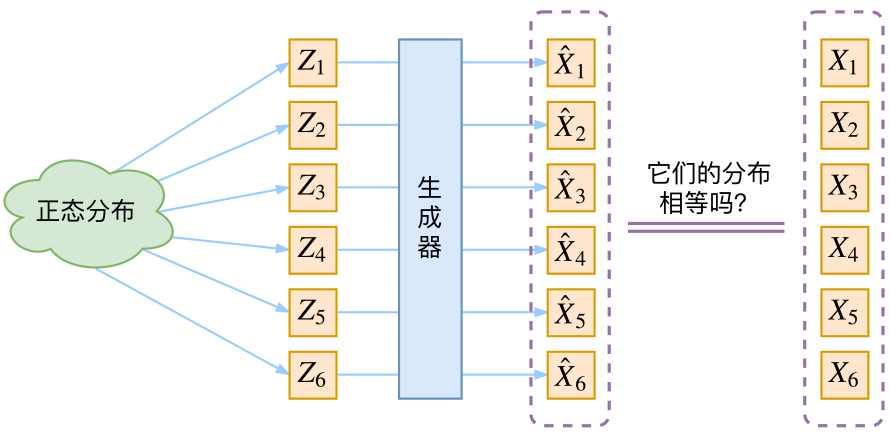
那现在假设\(Z\)服从标准的正态分布,那么就可以从中采样得到若干个\(Z_1,Z_2,...,Z_n\),然后对它做变换得到\(\hat{X_1}=g(Z_1), \hat{X_2}=g(Z_2), ..., \hat{X_n}=g(Z_n)\),我们怎么判断这个通过\(g\)构造出来的数据集,它的分布跟我们目标的数据集分布是不是一样的呢?有读者说不是有KL散度吗?当然不行,因为KL散度是根据两个概率分布的表达式来算它们的相似度的,然而目前我们并不知道它们的概率分布的表达式,我们只有一批从构造的分布采样而来的数据\(\hat{X_1}, \hat{X_2}, ..., \hat{X_n}\),还有一批从真实的分布采样而来的数据\(X_1, X_2, ..., X_n\)。我们只有样本本身,没有分布表达式,当然也就没有方法算KL散度。
虽然遇到困难,但还是要想办法解决的。GAN的思路很直接粗犷:既然没有合适的度量,那我干脆把这个度量也用神经网络训练出来吧。就这样,WGAN就诞生了。而VAE则使用了一个精致迂回的技巧。
VAE
这一部分我们先回顾一般教程是怎么介绍VAE的,然后再探究有什么问题,接着就自然地发现了VAE真正的面目。
经典回顾
首先我们有一批数据样本\(X_1, X_2, ..., X_n\),其整体用\(X\)来描述,我们本想根据\(X_1, X_2, ..., X_n\)得到\(X\)的分布\(p(X)\),如果能得到的话,那我直接根据\(p(X)\)来采样,就可以得到所有可能的\(X\)了(包括\(X_1, X_2, ..., X_n\)以外的),这是一个终极理想的生成模型了。当然,这个理想很难实现,于是我们将分布改一改:
\[p(X)=\sum_Z p(X|Z)p(Z)\]
这里我们就不区分求和还是求积分了,意思对了就行。此时\(p(X|Z)\)就描述了一个由\(Z\)来生成\(X\)的模型,而我们假设\(Z\)服从标准正态分布,也就是\(p(Z)= \mathcal N(0, I)\)。如果这个理想能实现,那么我们就可以先从标准正态分布中采样一个\(Z\),然后根据\(Z\)来算一个\(X\),也是一个很棒的生成模型。接下来就是结合自编码器来实现重构,保证有效信息没有丢失,再加上一系列的推导,最后把模型实现。框架的示意图如下:
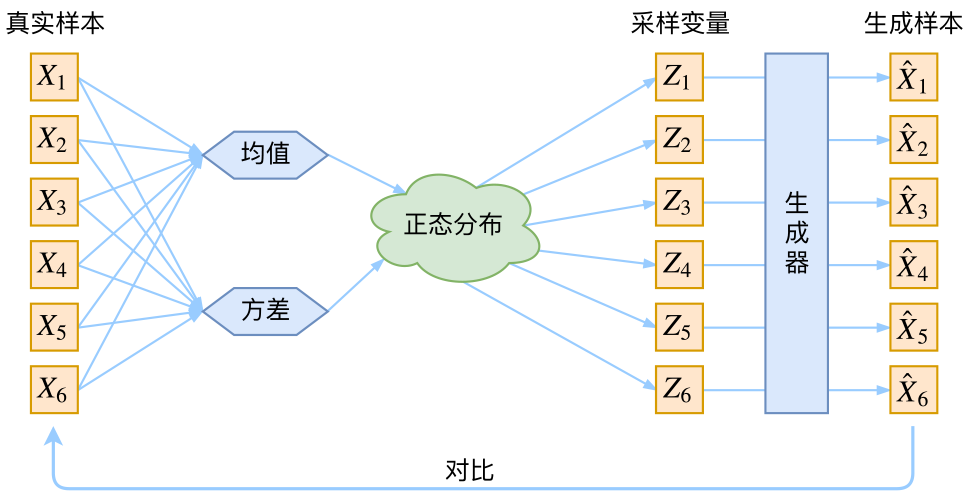
看出了什么问题了吗?如果像这个图的话,我们其实完全不清楚:究竟经过重新采样出来的\(Z_k\),是不是还对应着原来的\(X_k\),所以我们如果直接最小化\(D(\hat{X_k}, X_k)^2\)(这里\(D\) 代表某种距离函数)是很不科学的,而事实上你看代码也会发现根本不是这样实现的。
VAE初现
其实,在整个VAE模型中,我们并没有去使用\(p(Z)\)(隐变量空间的分布)是正态分布的假设,我们用的是假设\(p(Z|X)\)(后验分布)是正态分布!!
具体来说,给定一个真实样本\(X_k\),我们假设存在一个专属于\(X_k\)的分布\(p(Z|X_k)\),并进一步假设这个分布是正态分布。为什么要强调“专属”呢?因为我们后面要训练一个生成器\(X=g(Z)\),希望能够把从分布\(p(Z|X_k)\)采样出来的一个\(Z_k\)还原为\(X_k\)。如果假设\(p(Z)\)是正态分布,然后从\(p(Z)\)中采样一个\(Z\),那么我们怎么知道这个\(Z\)对应于哪个真实的\(X\)呢?现在\(p(Z|X_k)\)专属于\(X_k\),我们有理由说从这个分布采样出来的\(Z\)应该要还原到\(X_k\)中去。
这时候每一个\(X_k\)都配上了一个专属的正态分布,才方便后面的生成器做还原。但这样有多少个\(X\)就有多少个正态分布了。我们知道正态分布有两组参数:均值\(\mu\)和方差\(\sigma^2\)(多元的话,它们都是向量),那我怎么找出专属于\(X_k\)的正态分布\(p(Z|X_k)\)的均值和方差呢?好像并没有什么直接的思路。那好吧,那我就用神经网络来拟合出来吧!这就是神经网络时代的哲学:难算的我们都用神经网络来拟合。
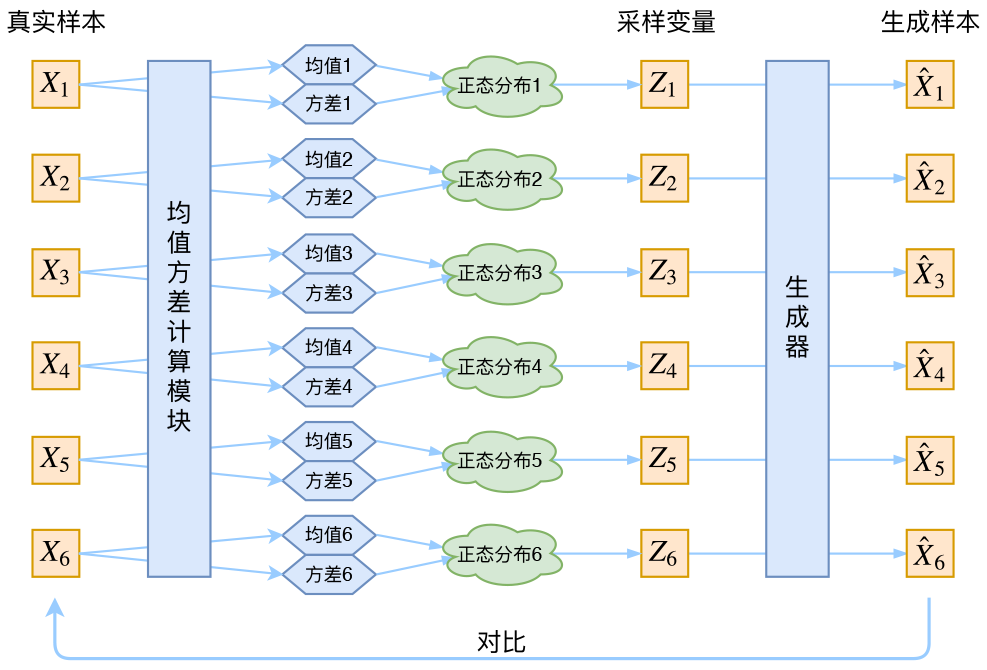
于是我们构建两个神经网络\(\mu_k=f_1(X_k),log \sigma_k^2=f_2(X_k)\)来算它们了。我们选择拟合\(log \sigma_k^2\)而不是直接拟合\(\sigma_k^2\),是因为\(\sigma_k^2\)总是非负的,需要加激活函数处理,而拟合\(log \sigma_k^2\)不需要加激活函数,因为它可正可负。到这里,我能知道专属于\(X_k\)的均值和方差了,也就知道它的正态分布长什么样了,然后从这个专属分布中采样一个\(Z_k\)出来,然后经过一个生成器得到\(\hat{X_k}=g(Z_k)\),现在我们可以放心地最小化\(D(\hat{X_k}, X_k)^2\),因为\(Z_k\)是从专属\(X_k\)的分布中采样出来的,这个生成器应该要把开始的\(X_k\)还原回来。于是可以画出VAE的示意图:
分布标准化
让我们来思考一下,根据上图的训练过程,最终会得到什么结果。
首先,我们希望重构\(X\),也就是最小化\(D(\hat{X_k}, X_k)^2\),但是这个重构过程受到噪声的影响,因为\(Z_k\)
是通过重新采样过的,不是直接由encoder算出来的。显然噪声会增加重构的难度,不过好在这个噪声强度(也就是方差)通过一个神经网络算出来的,所以最终模型为了重构得更好,肯定会想尽办法让方差为0。而方差为0的话,也就没有随机性了,所以不管怎么采样其实都只是得到确定的结果(也就是均值),只拟合一个当然比拟合多个要容易,而均值是通过另外一个神经网络算出来的。
说白了,模型会慢慢退化成普通的AutoEncoder,噪声不再起作用。
这样不就白费力气了吗?说好的生成模型呢?
别急别急,其实VAE还让所有的\(p(Z|X)\)都向标准正态分布看齐。
- 这样就防止了噪声为零(这样方差就不会为0,而是接近1)
- 同时保证了模型具有生成能力。怎么理解“保证了生成能力”呢?如果所有的\(p(Z|X)\)都很接近标准正态分布\(\mathcal N(0, I)\),那么根据定义:
\[p(Z)=\sum_X p(Z|X)p(X)=\sum_X \mathcal N(0, I)p(X)=\mathcal N(0, I)\sum_Xp(X)=\mathcal N(0, I)\]
这样我们就能达到我们的先验假设:\(p(Z)\)是标准正态分布。然后我们就可以放心地从\(\mathcal N(0, I)\)中采样来生成图像了。
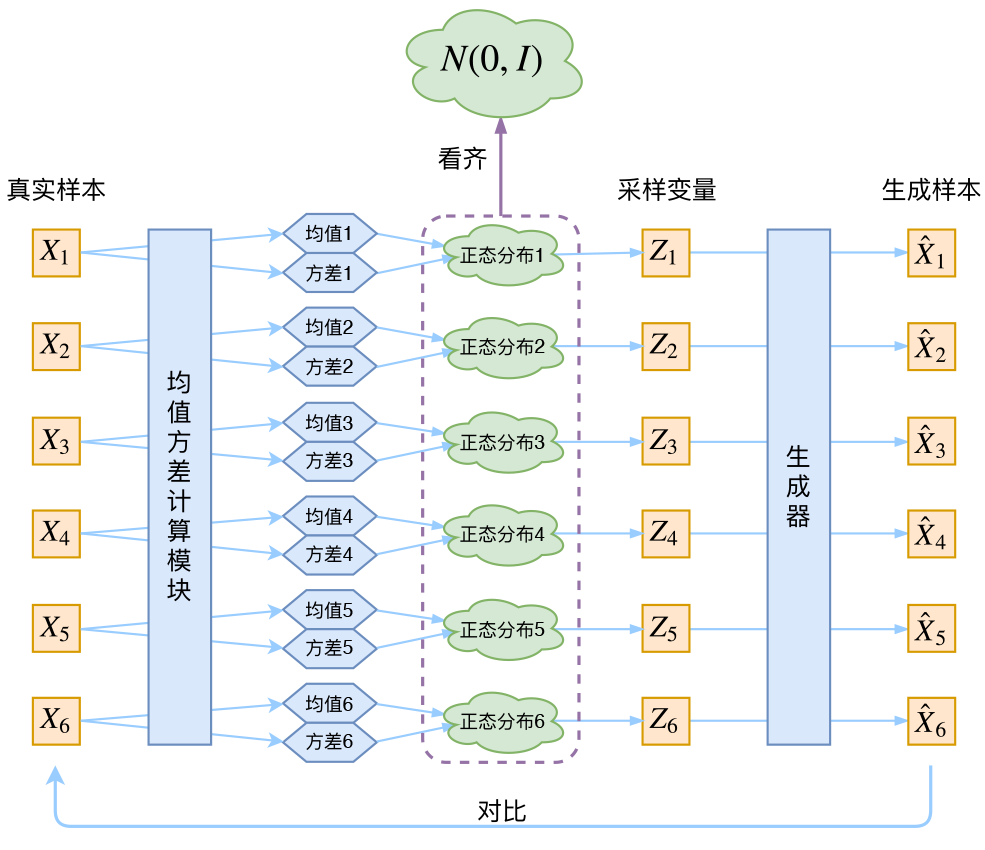
那怎么让所有的\(p(Z|X)\)都向\(\mathcal N(0, I)\)看齐呢?如果没有外部知识的话,其实最直接的方法应该是在重构误差的基础上中加入额外的loss:
\[L_{\mu}=\|f_1(X_k)\|^2, L_{\sigma^2}=\|f_2(X_k)\|^2\]
因为它们分别代表了均值\(\mu_k\)和方差的对数\(log \sigma_k^2\),达到\(\mathcal N(0, I)\)就是希望二者尽量接近于0了。不过,这又会面临着这两个损失的比例要怎么选取的问题,选取得不好,生成的图像会比较模糊。所以,原论文直接算了一般(各分量独立的)正态分布与标准正态分布的KL散度\(KL(\mathcal N(\mu, \sigma^2) \| \mathcal N(0, I))\)作为这个额外的loss,计算结果为:
\[L_{\mu,\sigma^2}=\frac{1}{2}\sum_{i=1}^{d}(\mu_{(i)}^2+\sigma_{(i)}^2-log \sigma_{(i)}^2-1)\]
重参数技巧
最后是实现模型的一个技巧,英文名是reparameterization trick,我这里叫它做重参数吧。其实很简单,就是我们要从\(p(Z|X_k)\)中采样一个\(Z_k\)出来,尽管我们知道了\(p(Z|X_k)\)是正态分布,但是均值方差都是靠模型算出来的,我们要靠这个过程反过来优化均值方差的模型,但是“采样”这个操作是不可导的,而采样的结果是可导的。我们利用
\[ \begin{align} & \frac{1}{\sqrt{2 \pi \sigma^2}}exp(-\frac{(z - \mu)^2}{2 \sigma^2})dz \\ = & \frac{1}{\sqrt{2 \pi}}exp(-\frac{1}{2}(\frac{z - \mu}{\sigma})^2)d(\frac{z - \mu}{\sigma}) \\ \end{align} \]
这说明\((z - \mu) / \sigma =
\epsilon\)是服从均值为0、方差为1的标准正态分布的,要同时把\(dz\)考虑进去,是因为乘上\(dz\)才算是概率,去掉\(dz\)是概率密度而不是概率。这时候我们得到:
从\(\mathcal N(\mu,
\sigma^2)\)中采样一个\(Z\),相当于从\(\mathcal N(0, I)\)中采样一个\(\epsilon\),然后让\(Z= \mu + \epsilon \times \sigma\)。
于是,我们将从\(\mathcal N(\mu,
\sigma^2)\)采样变成了从\(\mathcal N(0,
I)\)中采样,然后通过参数变换得到从\(\mathcal N(\mu,
\sigma^2)\)中采样的结果。这样一来,“采样”这个操作就不用参与梯度下降了,改为采样的结果参与,使得整个模型可训练了。
后续分析
即便把上面的所有内容都搞清楚了,面对VAE,我们可能还存有很多疑问。
本质是什么
VAE的本质是什么?VAE虽然也称是AE(AutoEncoder)的一种,但它的做法(或者说它对网络的诠释)是别具一格的。在VAE中,它的Encoder有两个,一个用来计算均值,一个用来计算方差,这已经让人意外了:Encoder不是用来Encode的,是用来算均值和方差的,这真是大新闻了,还有均值和方差不都是统计量吗,怎么是用神经网络来算的?
事实上,我觉得VAE从让普通人望而生畏的变分和贝叶斯理论出发,最后落地到一个具体的模型中,虽然走了比较长的一段路,但最终的模型其实是很接地气的:
它本质上就是在我们常规的自编码器的基础上,对encoder的结果(在VAE中对应着计算均值的网络)加上了“高斯噪声”,使得结果decoder能够对噪声有鲁棒性;而那个额外的KL loss(目的是让均值为0,方差为1),事实上就是相当于对encoder的一个正则项,希望encoder出来的东西均有零均值。
那另外一个encoder(对应着计算方差的网络)的作用呢?它是用来动态调节噪声的强度的。直觉上来想,当decoder还没有训练好时(重构误差远大于KL loss),就会适当降低噪声(KL loss增加),使得拟合起来容易一些(重构误差开始下降);反之,如果decoder训练得还不错时(重构误差小于KL loss),这时候噪声就会增加(KL loss减少),使得拟合更加困难了(重构误差又开始增加),这时候decoder就要想办法提高它的生成能力了。
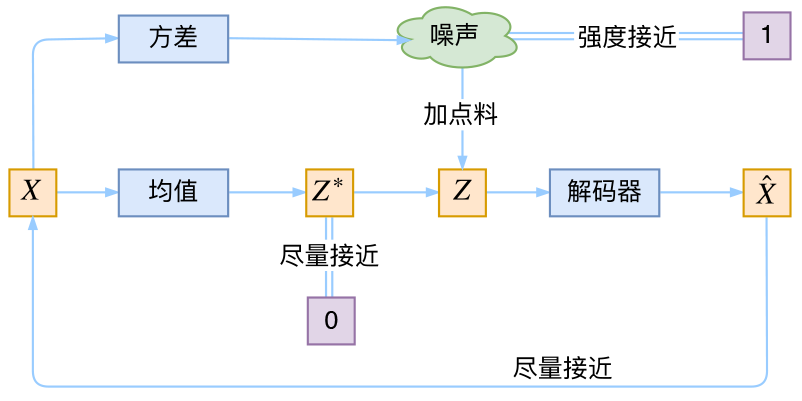
说白了,重构的过程是希望没噪声的,而KL loss则希望有高斯噪声的,两者是对立的。所以,VAE跟GAN一样,内部其实是包含了一个对抗的过程,只不过它们两者是混合起来,共同进化的。从这个角度看,VAE的思想似乎还高明一些,因为在GAN中,造假者在进化时,鉴别者是安然不动的,反之亦然。当然,这只是一个侧面,不能说明VAE就比GAN好。GAN真正高明的地方是:它连度量都直接训练出来了,而且这个度量往往比我们人工想的要好(然而GAN本身也有各种问题,这就不展开了)。
从这个讨论中,我们也可以看出,当然,每个\(p(Z|X)\)是不可能完全精确等于标准正态分布,否则\(p(Z|X)\)就相当于跟\(X\)无关了,重构效果将会极差。最终的结果就会是,\(p(Z|X)\)保留了一定的\(X\)信息,重构效果也还可以,并且
\[p(Z)=\sum_X p(Z|X)p(X)=\sum_X \mathcal N(0, I)p(X)=\mathcal N(0, I)\sum_Xp(X)=\mathcal N(0, I)\]
近似成立,所以同时保留着生成能力。
条件VAE
最后,因为目前的VAE是无监督训练的,因此很自然想到:如果有标签数据,那么能不能把标签信息加进去辅助生成样本呢?这个问题的意图,往往是希望能够实现控制某个变量来实现生成某一类图像。当然,这是肯定可以的,我们把这种情况叫做Conditional VAE,或者叫CVAE。(相应地,在GAN中我们也有个CGAN。)
但是,CVAE不是一个特定的模型,而是一类模型,总之就是把标签信息融入到VAE中的方式有很多,目的也不一样。这里基于前面的讨论,给出一种非常简单的VAE。
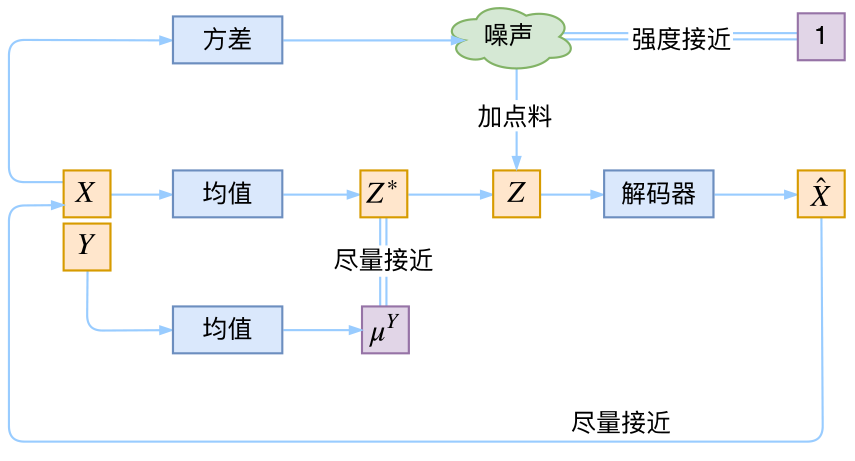
在前面的讨论中,我们希望\(X\)经过编码后,\(Z\)的分布都具有零均值和单位方差,这个“希望”是通过加入了KL loss来实现的。如果现在多了类别信息\(Y\),我们可以希望同一个类的样本都有一个专属的均值\(\mu^Y\)(方差不变,还是单位方差),这个\(\mu^Y\)让模型自己训练出来。这样的话,有多少个类就有多少个正态分布,而在生成的时候,我们就可以通过控制均值来控制生成图像的类别。事实上,这样可能也是在VAE的基础上加入最少的代码来实现CVAE的方案了,因为这个“新希望”也只需通过修改KL loss实现:
\[L_{\mu,\sigma^2}=\frac{1}{2}\sum_{i=1}^{d}((\mu_{(i)} - \mu_{(i)}^Y)^2+\sigma_{(i)}^2-log \sigma_{(i)}^2-1)\]