【文献阅读】RAG: Retrieval-Augmented Generation for Knowledge-Intensive NLP Tasks
论文地址:
论文代码:
RAG将问题求解划分为检索和生成两阶段:
- 先通过检索,查找与问题相关的文档。
- 将文档和问题一并输入生成模型,由模型推理给出最终的答案,从而解决模型无法扩展知识和产生“幻觉”的问题。
如问题:
美国现任总统是谁?
当使用不带有RAG的大模型时,输入输出为:
Input:美国现任总统是谁? Output:截至我的知识库更新时间2020年,美国现任总统是唐纳德·特朗普。
当使用带有RAG的大模型时,输入输出为:
Doc:美国现任(第46任)的总统为民主党籍的乔·拜登,于2021年1月20日上任,其搭档的副总统为同党的卡玛拉·哈里斯。 Input:美国现任总统是谁? Output:乔·拜登。
介绍
预训练语言模型可以从数据中学习知识,在不访问外部知识库的情况下,直接使用参数化的隐式知识库,但其存在以下缺点:
- 模型无法扩展或修改知识,比如用某天前的数据预训练的模型无法直接回答该天后发生的事。
- 模型可能产生“幻觉”,所有的AI模型的底层原理都是基于数学概率,其模型输出实质上是一系列数值运算,大模型也不例外,所以它有时候会一本正经地胡说八道,尤其是在大模型自身不具备某一方面的知识时或在不擅长的场景上更容易出错。而这种幻觉问题的区分是比较困难的,因为它要求使用者自身具备相应领域的知识。
因此,Facebook在2020年提出了RAG(Retrieval-Augmented Generation,检索增强生成)架构,该架构包含生成器与检索器两部分。
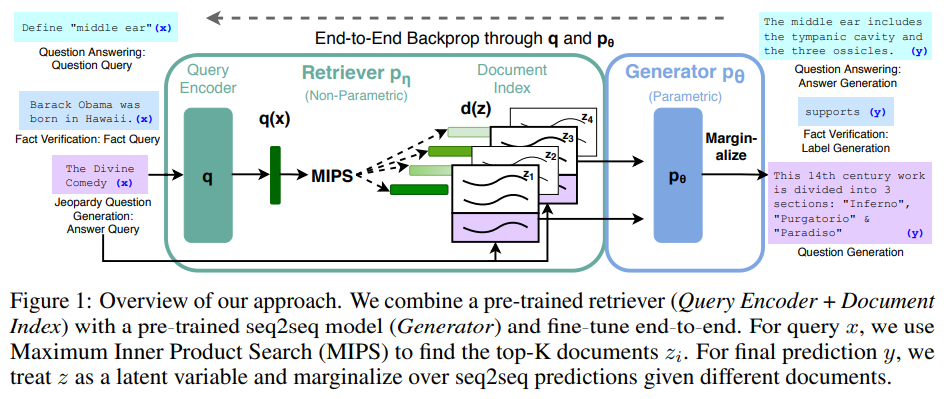
对于问答,RAG架构首先将问题输入检索器。检索器包含两个子部分:
查询编码器(Query Encoder):用\(q\)表示,其将问题进行向量化。文档索引(Document Index):用\(d\)表示,其将文档进行向量化,并构建文档向量索引。
问题输入检索器后,先通过查询编码器转化为问题向量,然后从文档向量索引中以最大内积搜索(Maximum Inner Product Search,MIPS)方式查找前K个文档。再将查找出的K个文档和问题合并输入生成器。生成器即预训练语言模型,其推理生成相应的问答。
方法
- 输入序列用\(x\)表示。
- 文档检索器为\(p_{\eta}(z|x)\),其根据\(x\)返回最相关的K个文档\(z\)。
- 生成器为\(p_{\theta}(y_i|x,z,y_{1:i-1})\),其通过自回归的方式,根据\(x\)和\(z\),以及前\(i-1\)个生成的token(\(y_{1:i-1}\)),预测当前token,直至生成完整的回答。
检索器
检索器可用如下公式表示:
\[d(z)=BERT_d(z)\] \[q(x)=BERT_q(x)\] \[p_{\eta}(z|x) \propto exp(d(z)^Tq(x))\]
其中,检索器的两个子部分均使用BERT模型,通过上述两个编码器分别得到问题和文档的向量。论文使用Faiss构建文档向量索引,并使用了HNSW算法对向量检索进行加速。向量检索的过程就是对问题和文档的向量求取内积作为相关度量,返回和问题向量内积最大、和问题最相关的前K个文档。
论文指出,检索器中的文档采用维基百科截至2018年12月的全量数据,将每篇维基百科文档切分为互不重叠的包含100个单词的块,每个块作为一个文档,共有2100万个文档。
生成器
生成器使用了Facebook发布的大语言模型BART-Large,其采用编码器+解码器架构,共有4亿个参数。
论文直接将问题和检索器返回的相关文档拼接在一起作为生成器的输入。
训练
论文采用端到端的方式对检索器和生成器进行联合训练,输入数据为文本对\((x,y)\)。
RAG-Sequence Model
\[p_{RAG-Sequence}(y|x) \approx \sum_{z \in top-k(p(\cdot|x))}p_{\eta}(z|x)p_{\theta}(y|x,z)=\sum_{z \in top-k(p(\cdot|x))}p_{\eta}(z|x)\prod_{i}^{N}p_{\theta}(y_i|x,z,y_{1:i-1})\]RAG-Token Model
\[p_{RAG-Token}(y|x) \approx \prod_i^N \sum_{z \in top-k(p(\cdot|x))} p_{\eta}(z|x)p_{\theta}(y_i|x,z,y_{1:i-1})\]
论文指出,训练时如果调整文档编码器所使用\(BERT_d\)模型的参数,则需要定期重新计算所有文档的向量并构建索引,成本较高且对效果提升不大。 因此,训练时,文档编码器所使用\(BERT_d\)模型的参数固定、不更新,而只对查询编码器所使用\(BERT_q\)模型和生成器所使用BART模型的参数进行更新。
扩展
对于构建一个RAG模型,我们可以将流程分为两步,分别为Database的构建和LLM的生成。
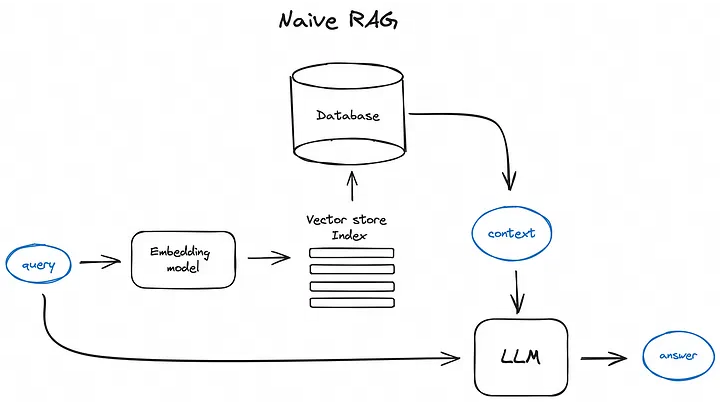
Database的构建
Faiss
Faiss是一个Facebook AI团队开源的库,全称为Facebook AI Similarity Search,该开源库针对高维空间中的海量数据(稠密向量),提供了高效且可靠的相似性聚类和检索方法,可支持十亿级别向量的搜索,是目前最为成熟的近似近邻搜索库。
HNSW(Hierarchcal Navigable Small World graphs)算法
KNN无法跟上速度
假设你有一本新书,你想在图书馆找到类似的书。k-最近邻(KNN)将浏览书架上的每一本书,并将它们从最相似到最不相似的顺序排列,以确定最相似的书。这样查找的时间是没有办法满足实时需求的。而且在真实应用中,图书馆有成千上万本书,每秒的找书请求也是成千上万的。这时KNN就更加没办法满足速度需求了。
如果我们对图书馆中的图书进行预排序和索引,这时要找到与你的新书相似的书,你所需要做的就是去正确的楼层,正确的区域,正确的通道找到相似的书。这一步骤大大减少了需要检查接近性的数据点的数量,使得检测时间大大缩短。这就是近似近邻(ANN)的思想。
HNSW就是一种ANN算法,下面对HNSW算法进行介绍。
朴素法
这里我们以一个小的场景为例来开始,假设我们现在有13个2维数据向量,我们把这些向量放在了一个平面直角坐标系内,隐去坐标系刻度,它们的位置关系如下图所示。
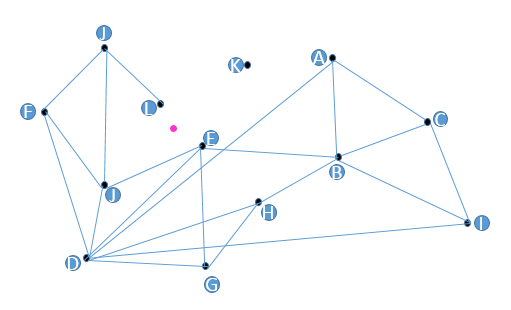
朴素查找法:
- 有一个很容易的的朴素想法,把某些点和点之间连上线,构成一个查找图,存下来备用;
- 当我想查找与粉色点最近的一点时,我从任意一个黑色点出发,计算它和粉色点的距离,与这个任意黑色点有连接关系的点我们称之为“友点”;
- 然后我要计算这个黑色点的所有“友点”与粉色点的距离,从所有“友点”中选出与粉色点最近的一个点,把这个点作为下一个进入点;
- 继续按照上面的步骤查找下去。如果当前黑色点对粉色点的距离比所有“友点”都近,终止查找,这个黑色点就是我们要找的离粉色点最近的点。
整个思想就是找出当前点及其邻近点与目标点之间的最近的那个点,然后把它当作当前点,再次循环。举个例子。
目标:我们要查找与粉色点最近的点。步骤:
- 从任意一个黑色点出发,这里我们随便选个C点吧,计算一下C点和粉色点的距离,存下来备用;
- 再计算C点的所有友点(A,I,B)与粉色点的距离(计算距离和度量的方式有多种,这里我们采用欧氏距离,就是二维物理空间上的“近和远”),我们计算得出B与粉色点的距离最近,而且B点距离粉色点的距离比C点距离粉色点的距离(前面算过)更近;
- 所以我们下面用B点继续查找。B点距离粉色点的距离保存下来,B点的友点是E,A,C,I,H,分别计算它们与粉色点的距离,得到E点与粉色点距离最近,且E点比B点距离粉色点还要近,所以我们选择E点作为下一个查找点。
- E点的友点是J,B,D,G,这时我们发现J点的与粉色点的距离最近,但是由于J点的距离粉色点的距离比E点还要远,所以满足了终止查找的条件,因此我们返回E点。
朴素想法之所以叫朴素想法就是因为它的缺点非常多。
- 首先,我们发现图中的K点是无法被查询到的,因为K点没有友点。
- 其次,如果我们要查找距离粉色点最近的两个点,而这两个近点之间如果没有连线,那么将大大影响效率(比如L和E点,如果L和E有连线,那么我们可以轻易用上述方法查出距离粉色点最近的两个点)。
- 最后一个大问题,D点真的需要这么多“友点”吗?谁是谁的友点应该怎么确定呢?
相关解决办法:
- 关于K点的问题,我们规定在构图时所有数据向量节点都必须有友点。
- 关于L和E的问题,我们规定在构图时所有距离相近(相似)到一定程度的向量必须互为友点。
- 关于D点问题,权衡构造这张图的时间复杂度,我们规定尽量减少每个节点的“友点”数量。
NSW算法
上述最后部分针对各个问题的解决办法促成了NSW算法的诞生。在图论中有一个很好的剖分法则专门解决上一节中提到的朴素想法的缺陷问题------德劳内(Delaunay)三角剖分算法,这个算法可以达成如下要求:
- 图中每个点都有“友点”。
- 相近的点都互为“友点”。
- 图中所有连接(线段)的数量最少。

如上图所示就是一个经典的满足上述三个条件的德劳内三角网图。但NSW没有采用德劳内三角剖分法来构成德劳内三角网图,原因是:
- 德劳内三角剖分构图算法时间复杂度太高,换句话说,构图太耗时。
- 德劳内三角形的查找效率并不一定最高,如果初始点和查找点距离很远的话我们需要进行多次跳转才能查到其临近点,需要“高速公路”机制(Expressway mechanism, 这里指部分远点之间拥有线段连接,以便于快速查找)。
在理想状态下,我们的算法不仅要满足上面三条需求,还要算法复杂度低,同时配有高速公路机制的构图法。
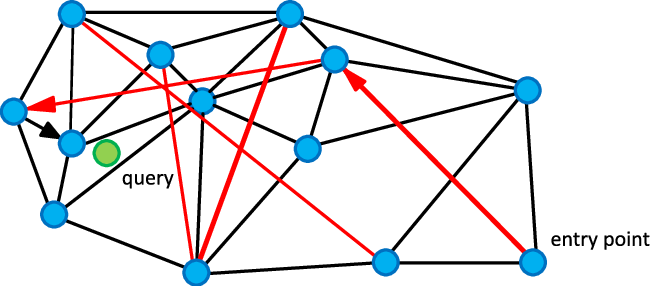
如上图所示,这是NSW论文中给出的一张满足条件的网络图,可以发现黑色是近邻点的连线,红色线就是“高速公路机制”了。我们从enter point点进入查找,查找绿色点临近节点的时候,就可以用过红色连线“高速公路机制”快速查找到结果。
NSW构图算法:
- 向图中逐个插入点,点的选取上随机的;
- 插入一个全新点时,通过朴素想法中的朴素查找法查找到与这个全新点最近的m个点(通过计算“友点”和待插入点的距离来判断下一个进入点是哪个点,m由用户设置);
- 连接全新点到m个点的连线。
仔细分析这个简单的构图方法,其中有一个精妙之处就是构图算法是逐点随机插入的,这就意味着在图构建的早期,很有可能构建出“高速公路”。
一个点,越早插入就越容易形成与之相关的“高速公路”连接,越晚插入就越难形成与之相关的“高速公路”连接。所以这个算法设计的妙处就在于扔掉德劳内三角构图法,改用“无脑添加”(NSW朴素插入算法),降低了构图算法时间复杂度的同时还带来了数量有限的“高速公路”,加速了查找。
假设我们现在要构成10000个点组成的图,设置m=4(每个点至少有4个“友点”),这10000个点中有两个点,p和q,他们俩坐标完全一样。假设在插入过程中我们分别在第10次插入p,在第9999次插入q,请问p和q谁更容易具有“高速公路”?答:因为在第10次插入时,只见过前9个点,故只能在前9个点中选出距离最近的4个点(m=4)作为“友点”,而q的选择就多了,前9998个点都能选,所以q的“友点”更接近q,p的早期“友点”不一定接近p,所以p更容易具有“高速公路”。

如上图所示就是一个构建好的NSW网络图,我们说明一下过程:
- 我们对7个二维点进行构图,用户设置m=3(每个点在插入时找3个紧邻友点)。
- 首先初始点是A点(随机出来的),A点插入图中只有它自己,所以无法挑选“友点”。
- 然后是B点,B点只有A点可选,所以连接BA,此为第1次构造。
- 然后插入F点,F只有A和B可以选,所以连接FA,FB,此为第2此构造。
- 然后插入了C点,同样地,C点只有A,B,F可选,连接CA,CB,CF,此为第3次构造。
- 重点来了,然后插入了E点,E点在A,B,F,C中只能选择3个点(m=3)作为“友点”,根据我们前面讲规则,要选最近的三个,怎么确定最近呢?朴素查找!从A,B,C,F任意一点出发,计算出发点与E的距离和出发点的所有“友点”和E的距离,选出最近的一点作为新的出发点,如果选出的点就是出发点本身,那么看我们的m等于几,如果不够数,就继续找第二近的点或者第三近的点,本着不找重复点的原则,直到找到3个近点为止。由此,我们找到了E的三个近点,连接EA,EC,EF,此为第四次构造。
- 第5次构造和第6次与E点的插入一模一样,都是在“现成”的图中查找到3个最近的节点作为“友点”,并做连接。
图画完了,请关注E点和A点的连线,如果我再这个图的基础上再插入6个点,这6个点有3个和E很近,有3个和A很近,那么距离E最近的3个点中没有A,距离A最近的3个点中也没有E,但因为A和E是构图早期添加的点,A和E有了连线,我们管这种连线叫“高速公路”,在查找时可以提高查找效率(当进入点为E,待查找距离A很近时,我们可以通过AE连线从E直接到达A,而不是一小步一小步分多次跳转到A)。
HNSW算法
HNSW算法就是跳表结构+NSW算法。
首先来看跳表结构。设有有序链表,名叫sorted_link,里面有n个节点,每个节点是一个整数。我们从表头开始查找,查找第t个节点需要跳转几次?答:t-1次。把n个节点分成n次查找的需求,都查找一遍,需要跳转几次?答: (0+1+2+3+.....+(n-1))次。如果我这链表长成下图这样呢?
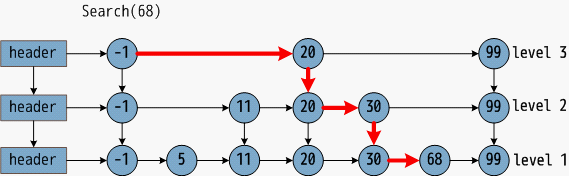
这已经不是一个有序链表了,这是三个有序链表+分层连接指针构成的跳表了。看这张示意图就能明白它的查找过程,先查第一层,然后查第二层,然后查第三层,然后找到结果。如果把上段所描述的名字叫sorted_link的链表建立成这样的跳表,那么把sorted_link中的所有元素都查一遍还需要花费(0+1+2+3+.....+(n-1))次吗?当然不需要。
跳表怎么构建呢?三个字,抛硬币。对于sorted_link链表中的每个节点进行抛硬币,如抛正,则该节点进入上一层有序链 表,每个sorted_link中的节点有50%的概率进入上一层有序链表。将上一层有序链表中和sorted_link链表中相同的元素做一一对应的指针链接。再从sorted_link上一层链表中再抛硬币,sorted_link上一层链表中的节点有50%的可能进入最表层,相当于sorted_link中的每个节点有25%的概率进入最表层。以此类推。
这样就保证了表层是“高速通道”,底层是精细查找,这个思想被应用到了NSW算法中,变成了其升级版-----HNSW。
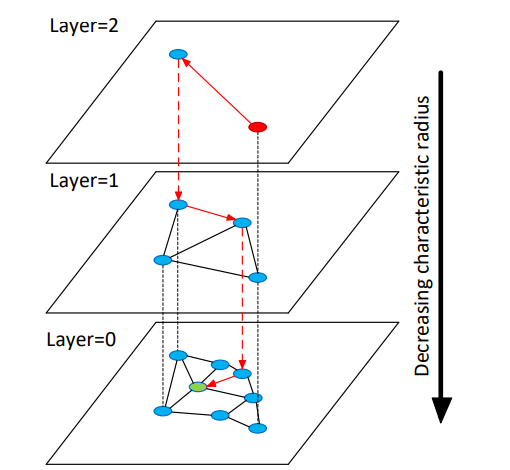
其中,Layer0中包含了数据集中的所有点,Layer1和Layer2是“高速通道”,越往高层越稀疏。
LLM的生成
在RAG中,大模型可以重新训练(针对特殊的输入格式进行微调)也可以不重新训练(通过prompt进行调整)。
重新训练(针对特殊的输入格式进行微调)
RAG-Sequence Model
\[p_{RAG-Sequence}(y|x) \approx \sum_{z \in top-k(p(\cdot|x))}p_{\eta}(z|x)p_{\theta}(y|x,z)=\sum_{z \in top-k(p(\cdot|x))}p_{\eta}(z|x)\prod_{i}^{N}p_{\theta}(y_i|x,z,y_{1:i-1})\]RAG-Token Model
\[p_{RAG-Token}(y|x) \approx \prod_i^N \sum_{z \in top-k(p(\cdot|x))} p_{\eta}(z|x)p_{\theta}(y_i|x,z,y_{1:i-1})\]
不重新训练(通过prompt进行调整)
1 | def question_answering(context, query): |