MinHash算法

MinHash算法和LSH（Locality Sensitive Hashing），用于快速估计两个集合的相似度。它们被广泛应用于大数据集的相似检索、推荐系统、聚类分析中，如今在大模型预训练的数据处理中也有使用到这两个算法。

MinHash

MinHash算法主要工作是对输入的高维向量（可能是几百万维甚至更高）转换为低维的向量（降维后的向量被称作数字签名），然后再对低维向量计算其相似，以达到降低计算成本，提高运行效率的目的, 我们接下来需要关注的就是MinHash是如何实现上述需求的了。

Jaccard 相似度

Jaccard相似度计算的是两个集合的相似性， 两个集合中，交集的个数/并集的个数。

定义集合A和B的的 Jaccard 系数为

\[J(A, B)=\frac{A \cap B}{A \cup B}\]

假设有如下集合，

\[ \begin{align} S_1 =& \{1,2,5\} \\ S_2 =& \{3\} \\ S_3 =& \{2,3,4,6\} \\ \end{align} \]

集合\(S_1\)和\(S_3\)之间的 Jaccard similarity 为

\[J(S_1, S_3)=\frac{|\{2\}|}{|\{1,2,3,4,5,6\}|}=\frac{1}{6}\]

当处理文本时，两个集合可以是两个文本的字集合，也可以是分词后的词集合，如果词集合太大，也可以先用TF-IDF筛选出比较重要的关键词作为词集。

Jaccard相似度和汉明距离类似的，只不过汉明距离考虑位置信息，而Jaccard相似度不考虑位置。

MinHash降维

海量文本直接求Jaccard相似度复杂度太高，两个文档需要逐个词比较（此时词的维度可能是几百万维甚至更高），为降低复杂度，我们使用两个文档的最小哈希值相等的概率来等价于两个文档的Jaccard相似度，并可以证明两者是相等的。

---

首先说明一下如何求一个集合的最小哈希值，假设现在有4个集合，分别为\(S_1, S_2, S_3, S_4\)；其中，\(S_1=\{a, d\}\)，\(S_2=\{c\}\)，\(S_3=\{b, d, e\}\)，\(S_4=\{a, c, d\}\)，所以全集\(\cup = \{a, b, c, d, e\}\)。我们可以构造如下0-1矩阵：

元素	\(S_1\)	\(S_2\)	\(S_3\)	\(S_4\)
a	1	0	0	1
b	0	0	1	0
c	0	1	0	1
d	1	0	1	1
e	0	0	1	0

为得到各集合的最小哈希值，首先对矩阵进行随机行打乱，则某个集合（某一列）的最小哈希值就等于打乱后第一个值为1的行所在的行号。定义一个最小哈希函数h，用于模拟对矩阵进行随机打乱，假设打乱后的矩阵如下表所示：

元素	\(S_1\)	\(S_2\)	\(S_3\)	\(S_4\)
b	0	0	1	0
e	0	0	1	0
a	1	0	0	1
d	1	0	1	1
c	0	1	0	1

则\(h(S_1)=2,h(S_2)=4,h(S_3)=0,h(S_4)=2\)。

重复上述随机行打乱和计算最小哈希值的过程，这样我们就可以得到一个签名矩阵，签名矩阵里记录着不同打乱顺序下各个集合的最小哈希值，如下表所示：

打乱顺序	\(S_1\)	\(S_2\)	\(S_3\)	\(S_4\)
\(h_1\)	1	3	0	1
\(h_2\)	0	2	0	0
...	...	...	...	...
\(h_n\)	2	4	0	2

通过签名矩阵，我们可以计算h(\(S_1\))=h(\(S_2\))的概率，两个文档的最小哈希值相等的概率来等价于两个文档的Jaccard相似度。

h(\(S_1\))和h(\(S_2\))相等的概率为\(\frac{\sum_{i=1}^{n}h_i(S_1)=h_i(S_2)}{n}\)，这里\(n<<特征维度\)，所以可以降低计算量。

---

经过随机打乱后，两个集合的最小哈希值相等的概率=两集合的Jaccard的相似度证明如下：

考虑集合\(S_1\)和\(S_2\)，这两列所在的行有以下三种情况：

1. \(S_1\)和\(S_2\)的值都为1，用X表示；
2. \(S_1\)和\(S_2\)的值一个为1,一个为0，用Y表示；
3. \(S_1\)和\(S_2\)的值都为0,用Z表示。

1. \(S_1\)与\(S_2\)的交集元素个数为X，并集个数为X+Y，所以Jaccard(\(S_1\),\(S_2\))=X/(X+Y)。
2. 随机打乱后h(\(S_1\))=h(\(S_2\))的概率等于从上往下扫描，在遇到Y行之前遇到X行的概率（Z行没有影响），或者说把X个黑球和Y个白球放入一个袋子中，首次拿到黑球的概率，即h(\(S_1\))=h(\(S_2\))的概率为X/(X+Y)。

当特征矩阵很大时，对其进行打乱非常耗时，而且要进行多次打乱，所以在实际使用中，通过多个随机哈希函数来模拟打乱的效果。具体的步骤如下：

1. 定义n个随机哈希函数\(h_1, h_2, ..., h_n\)，例如\(h_1(x) = (x+1)%m（m是行数）\)。
2. 计算\(h_1(r), h_2(r), ..., h_n(r)\)对应下图中的\(Permutation \pi\)。
3. 对第i个哈希函数\(h_i\)，在集合\(S_j\)上更新签名矩阵，\(sig(i, j)=min(sig(i, j), h_i(r)),if 特征值为1，r=0,1,...,m(m为特征数)\)。

注：下图中Permutation下标从1开始。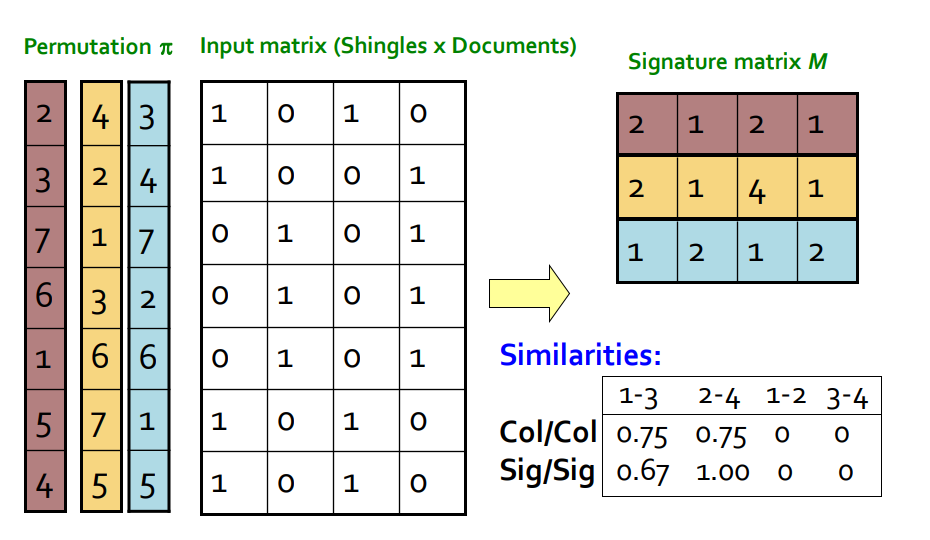

LSH（Locality Sensitive Hashing）

MinHash降低了两个高维向量之间的计算复杂性，但还有一个需要考虑的问题是，我们需要对大量的向量之间进行两两比较，如果每个都直接比较，复杂度是\(O(N^2)\)（N是向量个数），是否有一种方法，将潜在的可能相似度高的向量聚在一起，将相似度低的向量分开？

LSH(Locality Sensitive Hashing)做的就是这个事情，其基本思想为：我们不需要去比对所有的文档，将所有的文档(columns) hash到许多桶中，形成候选匹配对，只有同一个桶中的signature会进行匹配。

---

LSH将原signature matrix按行划分成多个band，每个band的宽度是r，显然有b*r=num of hash function for MinHash，然后对band内每个signature段hash，形成多个桶，如下图:

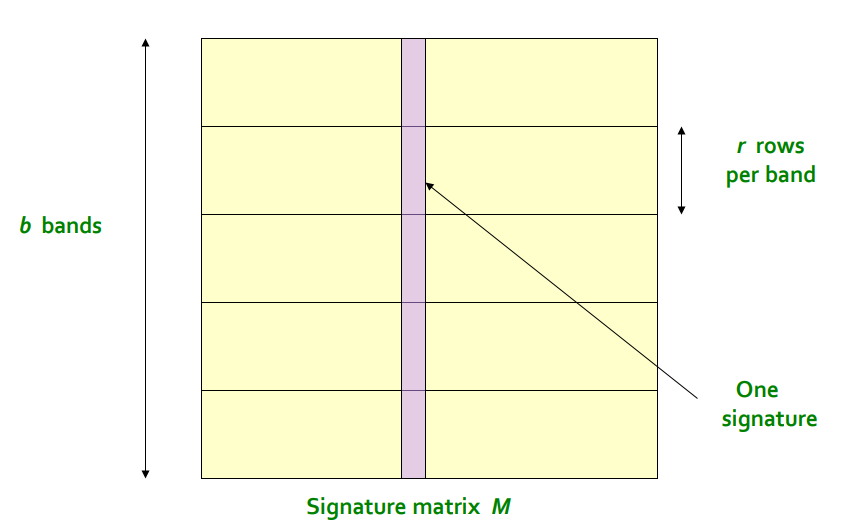
两个文档作为候选匹配的充要条件是至少有一个band的hash在同一个桶中。

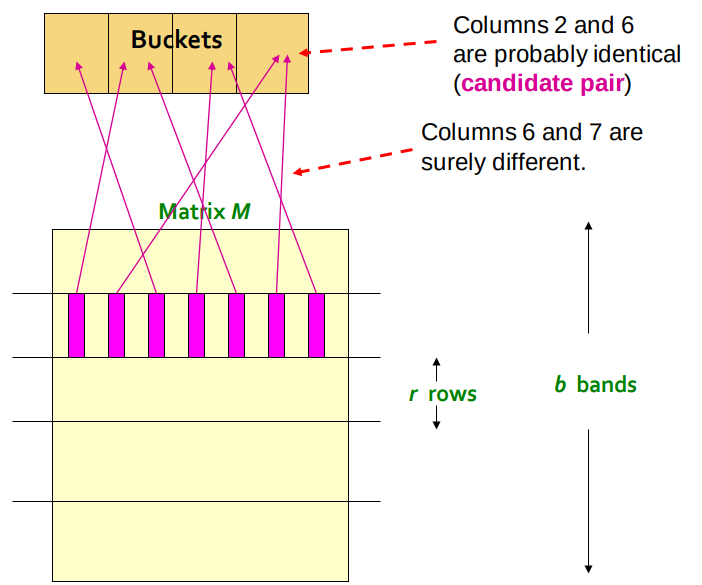
但hash分桶的时候仍然存在可能分错桶的情况，分别是：

• 本应认定不相似的分到了一个桶中：因为有小部分MinHash会相同的概率。
• 本应认定相似的没分到一个桶中：每个band Hash的结果刚好都不一样。

设s代表两个文档相似度（对应MinHash相同的概率），那么有：

• 一个band内所有行都相等的概率：\(s^r\)
• 一个band内至少有一行(一个MinHash)不相等的概率：\(1-s^r\)
• 所有band都不相等的概率：\((1-s^r)^b\)
• 至少有一个band相等的概率：\(1-(1-s^r)^b\)

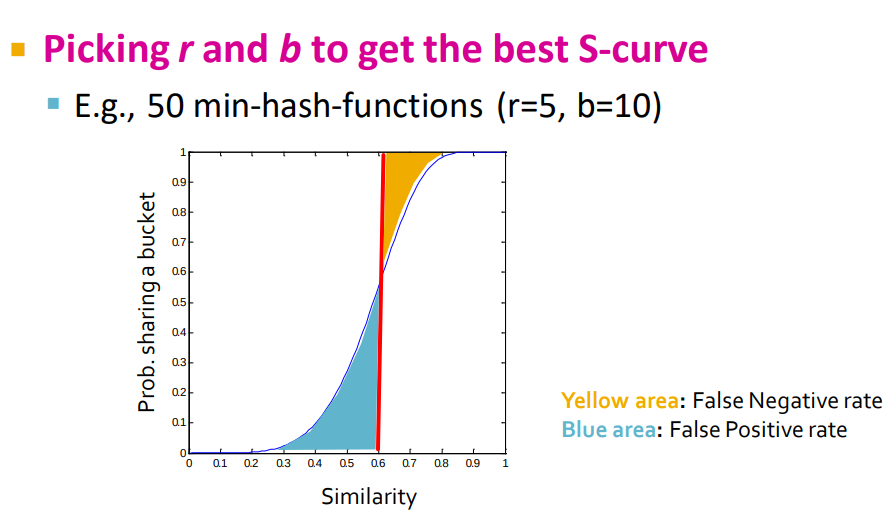
其中，至少有一个band相等的概率\(1-(1-s^r)^b\)实际上就对应文档被划分到一个桶中的概率。两个文档相似度不同时，其对应概率的变化如下表(取r=5,b=20)：

s	\(1-(1-s^r)^b\)
0.2	0.006
0.3	0.047
0.4	0.186
0.5	0.470
0.6	0.802
0.7	0.975
0.8	0.9996

可以看出，相似度越大，越容易被hash到同一个桶中。通过设置合适的\(r,b\)超参数，我们可以将相似的文档尽可能分到同一个桶中，而不相似文档尽可能不在相同的桶中，如下图所示。