MLA(Multi-head Latent Attention)详解
在DeepSeek的模型层面,有两个值得关注的点:
- Multi-head Latent
Attention(MLA):这个结构对传统Transformer中的MHA结构进行改进,主要目标有两个:
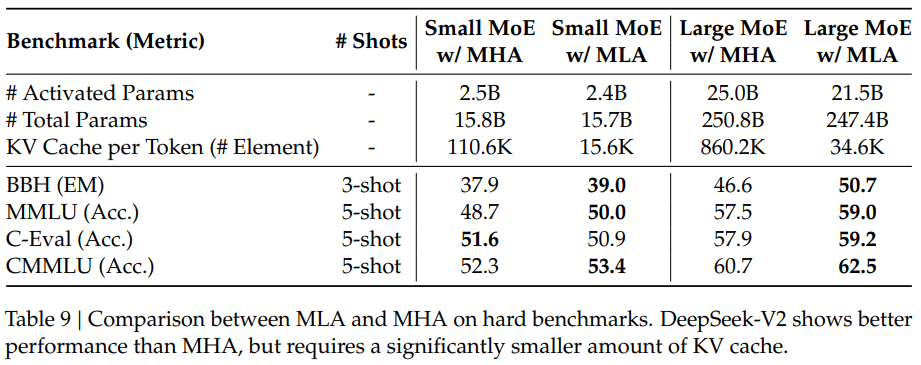
- 降低推理时KV Cache的存储开销;
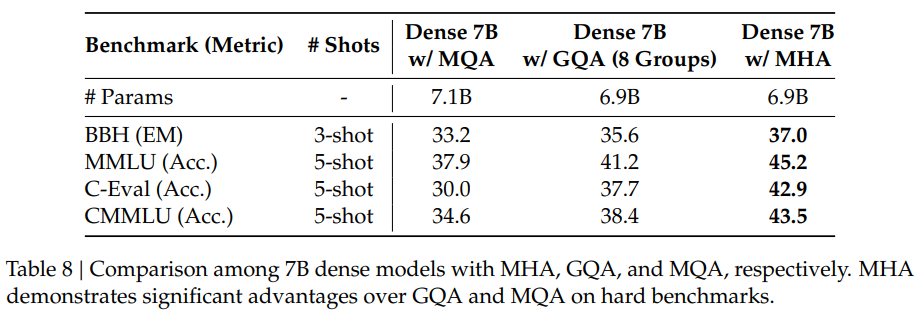
- 缓解GQA和MQA等方法导致的模型性能损耗。
- DeepSeekMoE:这部分结构和DeepSeek-MoE 中保持一致,两个核心思想是:
- Fine-grained Expert Segmentation,即将FFN中间层隐层维度拆分成多个更小的维度;
- Shared Expert Isolation,设置共享专家捕获常识性知识。
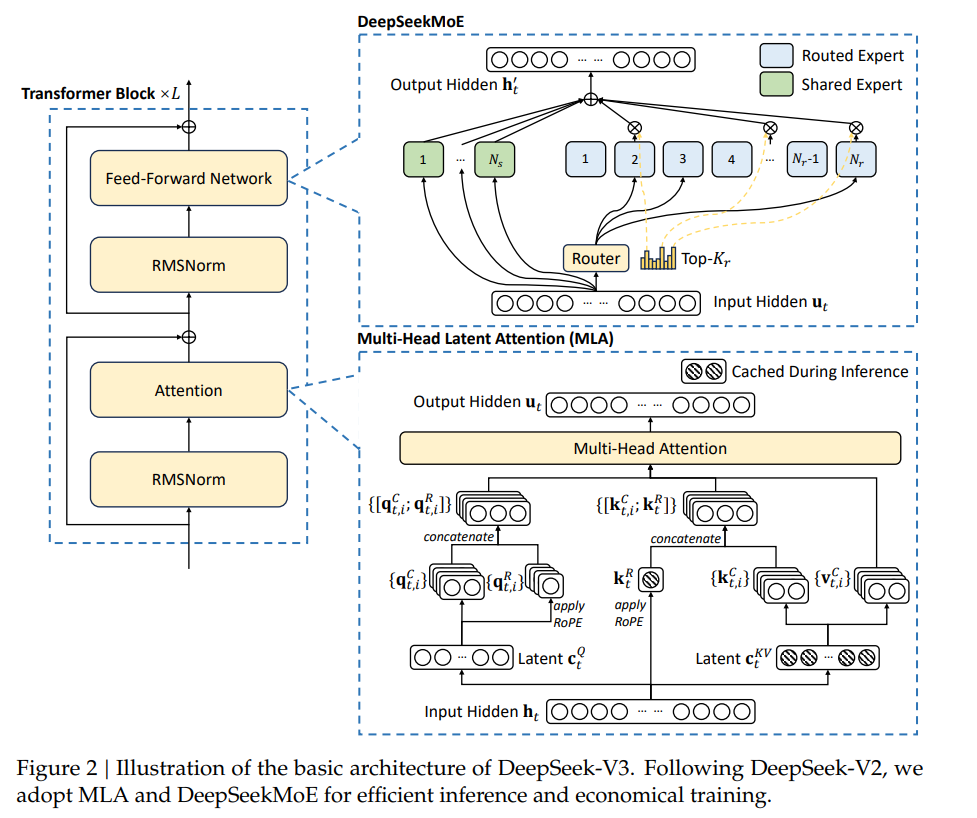
这篇文章先来说第一个部分, MLA(Multi-head Latent Attention)算法的原理。
标准的MHA结构
MHA(即多头注意力机制)是在Transformer原始论文中提出的。这里设\(d\)表示embedding的维度,\(n_h\)表示attention heads的数量,\(d_h\)表示每一个头的维度,\(h_t \in \mathbb{R}^d\)表示第\(t\)个token在一个attention层的输入。那么通过3个参数矩阵\(W^Q, W^K, W^V \in \mathbb{R}^{d_hn_h \times d}\)就可以得到\(q_t, k_t, v_t \in \mathbb{R}^{d_hn_h}\),即:
\[ \begin{align} q_t = W^Qh_t \\ k_t = W^Kh_t \\ v_t = W^Vh_t \end{align} \]
在多头注意力计算中,这里的\(q_t, k_t, v_t \in \mathbb{R}^{d_hn_h}\)会分割成\(n_h\)个注意力头,即:
\[ \begin{align} [q_{t,1};q_{t,2};...;q_{t,n_h}] = q_t \\ [k_{t,1};k_{t,2};...;k_{t,n_h}] = k_t \\ [v_{t,1};v_{t,2};...;v_{t,n_h}] = v_t \\ o_{t,i} = \sum_{j=1}^{t}Softmax_j(\frac{q_{t,i}^{\top}k_{j,i}}{\sqrt{d_h}})v_{j,i} \\ u_t = W^O[o_{t,1};o_{t,2};...;o_{t,n_h}] \end{align} \]
这里\(q_{t,i},k_{t,i},v_{t,i} \in \mathbb{R}^{d_h}\)分别表示query、key、value的第\(i\)个attention head,\(W^O \in \mathbb{R}^{d \times d_hn_h}\)表示输出映射矩阵。那么如果模型结构是MHA,在推理时,KV Cache对于每个token需要缓存的参数有\(2n_hd_hl\)(l表示网络层数)。
为了缓解推理时KV Cache显存占用的问题,相继出现了Multi-Query Attention (MQA) 和 Grouped-Query Attention (GQA) 等方法,这些方法降低了KV Cache的容量,但同时也导致模型整体性能会有一定程度的下降。
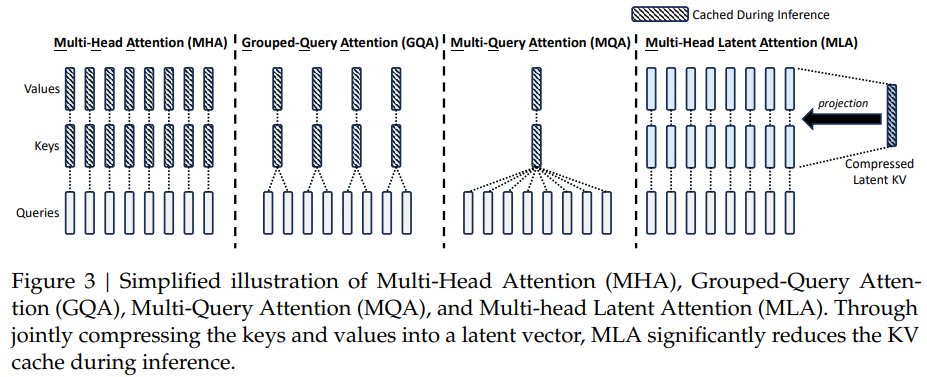
MLA结构
MLA的核心是对keys和values进行低秩联合压缩,从而降低KV Cache。
\[ \begin{align} c_t^{KV} = W^{DKV}h_t \\ k_t^{C} = W^{UK}c_t^{KV} \\ v_t^{C} = W^{UV}c_t^{KV} \end{align} \]
其中:
- \(c_t^{KV} \in \mathbb{R}^{d_c}\):表示对keys和values压缩后的隐向量latent vector,这里\(d_c(<<d_hn_h)\)表示KV压缩的维度。
- \(W^{DKV} \in \mathbb{R}^{d_c \times d}\):表示降维映射down-projection矩阵,将\(d\)维向量降维到\(d_c\)。
- \(W^{UK},W^{UV} \in \mathbb{R}^{d_hn_h \times d_c}\):表示升维映射up-projection矩阵,将\(d_c\)维向量升维到\(d_hn_h\)。
这样在推理时,只需要缓存隐向量\(c_t^{KV}\)即可,这样MLA对应的每一个token的KV Cache参数只有\(d_cl\)个。
此外,为了降低训练过程中的激活内存activation memory,DeepSeek还对queries进行低秩压缩,即便这并不能降低KV Cache:
\[ \begin{align} c_t^{Q} = W^{DQ}h_t \\ q_t^{C} = W^{UQ}c_t^Q \end{align} \]
其中:
- \(c_t^Q \in \mathbb{R}^{d_c^{\prime}}\):表示将queries压缩后的隐向量,\(d_c^{\prime}(<<d_hn_h)\)表示压缩后的维度。
- \(W^{DQ} \in \mathbb{R}^{d_c^{\prime} \times d}, W^{UQ} \in \mathbb{R}^{d_hn_h \times d_c^{\prime}}\):分别表示down-projection和up-projection矩阵。
这里有一个技巧,因为缓存的是\(c_t^{KV}\),在计算注意力时如果还用原来的方法,则需要通过\(W^{UK},W^{UV}\)重新计算出\(k_t^{C},v_t^{C}\),增加大量推理开销。 MLA在推理时将\(W^{UK},W^{UV}\)分别融入到模型权重\(W^Q,W^O\)里,从而不带来额外的推理开销。
对于\({q_t^C}^{\top}k_j^C\)的计算:
\[ \begin{align} {q_t^C}^{\top}k_j^C &= (W^{UQ}c_t^Q)^{\top}W^{UK}c_j^{KV} \\ &= {c_t^Q}^{\top}((W^{UQ})^{\top}W^{UK})c_j^{KV} \end{align} \]
将\((W^{UQ})^{\top}W^{UK}\)视为一个合并后的矩阵,用它进行推理阶段的计算即可,这时只需用到\(c_t^{KV}\),不需重新计算\(k_t^{C}\)。
对于注意力输出的计算:
\[ \begin{align} u_t &= W^O\sum_{j=1}^{t}Softmax_j(\frac{q_t^{\top}k_j^C}{\sqrt{d_h}})v_j^C \\ &= W^O\sum_{j=1}^{t}Softmax_j(\frac{q_t^{\top}k_j^C}{\sqrt{d_h}})W^{UV}c_j^{KV} \\ &= \sum_{j=1}^{t} \text{Softmax}_j\left( \frac{q_t^{\top} k_j^C}{\sqrt{d_h}} \right) (W^O W^{UV}) c_j^{KV} \end{align} \]
将\(W^O W^{UV}\)视为一个合并后的矩阵,用它进行推理阶段的计算即可,这时只需用到\(c_t^{KV}\),不需重新计算\(v_t^{C}\)。
融入RoPE
上面的过程中,我们丢失了一个非常重要的步骤,即位置编码RoPE。
原始的RoPE需要在query和key中融入相对位置信息。在MLA中,在query中融入相对位置信息是比较容易的。但是对于key,Cache缓存的是压缩后的低秩kv信息,而RoPE要在\(q、k\)做内积之前进行旋转,这将导致\(W^{UK}\)无法融入到\(W^Q\)中, 每次推理时都需要重新从\(c_t^{KV}\)计算\(k_t^{C}\),从而增加大量推理开销。
加入RoPE之后,对于\({q_t^C}^{\top}k_j^C\)的计算变成如下形式:
\[ \begin{align} {q_t^C}^{\top}k_j^C &= (R_tW^{UQ}c_t^Q)^{\top} \times R_jW^{UK}c_j^{KV} \\ &= {c_t^Q}^{\top}(W^{UQ})^{\top}R_t^{\top}R_jW^{UK}c_j^{KV} \\ &= {c_t^Q}^{\top}(W^{UQ})^{\top}R_{t-j}W^{UK}c_j^{KV} \end{align} \]
其中,\((W^{UQ})^{\top}R_{t-j}W^{UK}\)是随着相对位置变化而变化的,并不是个固定矩阵,因此不能提前计算好。
为此,MLA 采用 decoupled RoPE,使用额外的queries \(q_{t,i}^R \in \mathbb{R}^{d_h^R}\)以及共享的key \(k_t^R \in \mathbb{R}^{d_h^R}\)来携带RoPE信息。
此时需要缓存\(c_t^{KV}\)和\(k_t^R\),所需的KV Cache变为\((d_c + d_h^R)l\)
基于这种解偶的RoPE策略,MLA遵循的计算逻辑为:
\[ \begin{align} [q_{t,1}^R;q_{t,2}^R;...;q_{t,n_h}^R] = q_t^R &= RoPE(W^{QR}c_t^Q) \\ k_t^R &= RoPE(W^{KR}h_t) \\ q_{t,i} &= [q_{t,i}^C;q_{t,i}^R] \\ k_{t,i} &= [k_{t,i}^C;k_t^R] \\ o_{t,i} &= \sum_{j=1}^tSoftmax_j(\frac{q_{t,i}^{\top}k_{j,i}}{\sqrt{d_h + d_h^R}})v_{j,i}^C \\ u_t &= W^O[o_{t,1};o_{t,2};...;o_{t,n_h}] \end{align} \]
其中:
- \(W^{QR} \in \mathbb{R}^{d_h^Rn_h \times d_c^{\prime}}\)和\(W^{KR} \in \mathbb{R}^{d_h^R \times d}\)分别表示计算解耦后的queries和key的矩阵。
- RoPE(...)表示应用RoPE的操作。
MLA效果