PPO&GRPO
详解PPO算法和GRPO算法。
强化学习的概念
- State: 状态,表示当前的局面,如果是LLM那就是一个句子(可以是不完整的句子),用\(s\)表示。
- Action: 动作,在当前局面下作出的反应,如果是LLM那就是生成一个token,用\(a\)表示。
- Action Space: 动作空间,可选择的动作,在LLM中就是可以输出的所有token。
- Policy: 策略函数,输入State,输出Action的概率分布,一般用\(\pi\)表示。
- Trajectory: 轨迹,一连串状态和动作的序列。表示为\(\tau = s_0, a_0, s_1, a_1, ....\)。
- Reward: 当前时间点的奖励。
- Return: 回报,从当前时间点到结束的Reward的累计和。
期望计算方式:
- 每个可能结果的概率与其结果值的乘积之和。
- 采样多次取平均值。(约等于,采样次数趋于无穷时取等号)
\[E(x)_{x \sim p(x)}=\sum_{x}x * p(x) \approx \frac{1}{n}\sum_{i=1}^{n}{x_i}\]
强化学习的目标:训练一个Policy(神经网络\(\pi\)),在所有的状态s下,给出相应的Action,使得到的Return期望最大。
基础知识
将上面强化学习的目标变为公式,一步一步计算。
Return的期望表示为:
\[E(R(\tau))_{\tau \sim P_{\theta}(\tau)}=\sum_{\tau}R(\tau)P_{\theta}(\tau)\]
因为要对上面的期望求最大值,所以对上式求梯度:
\[ \begin{align} \nabla E(R(\tau))_{\tau \sim P_{\theta}(\tau)}&=\nabla \sum_{\tau}R(\tau)P_{\theta}(\tau) \\ &=\sum_{\tau}R(\tau) \nabla P_{\theta}(\tau) \\ &=\sum_{\tau}R(\tau) \nabla P_{\theta}(\tau) \frac{P_{\theta}(\tau)}{P_{\theta}(\tau)} \\ &=\sum_{\tau}P_{\theta}(\tau)R(\tau) \frac{\nabla P_{\theta}(\tau)}{P_{\theta}(\tau)} \end{align} \]
这里将\(R(\tau) \frac{\nabla P_{\theta}(\tau)}{P_{\theta}(\tau)}\)看作一个整体,则概率\(P_{\theta}(\tau)\)和这个整体的乘积可表示为期望,用期望计算方式二来变换上式得到:
数学技巧:\(\nabla logf(x)=\frac{\nabla f(x)}{f(x)}\)
\[ \begin{align} \nabla E(R(\tau))_{\tau \sim P_{\theta}(\tau)}&=\sum_{\tau}P_{\theta}(\tau)R(\tau) \frac{\nabla P_{\theta}(\tau)}{P_{\theta}(\tau)} \\ & \approx \frac{1}{N}\sum_{n=1}^{N}R(\tau^n) \frac{\nabla P_{\theta}(\tau^n)}{P_{\theta}(\tau^n)} \\ &=\frac{1}{N}\sum_{n=1}^{N}R(\tau^n) \nabla logP_{\theta}(\tau^n) \end{align} \]
更进一步,我们将上式中的Trajectory拆分细化:
\[ \begin{align} \nabla E(R(\tau))_{\tau \sim P_{\theta}(\tau)}&=\frac{1}{N}\sum_{n=1}^{N}R(\tau^n) \nabla logP_{\theta}(\tau^n) \\ &=\frac{1}{N}\sum_{n=1}^{N}R(\tau^n) \nabla log \prod_{t=1}^{T_n}P_{\theta}(a_n^t|s_n^t) \\ &=\frac{1}{N}\sum_{n=1}^{N}R(\tau^n) \sum_{t=1}^{T_n} \nabla logP_{\theta}(a_n^t|s_n^t) \\ &=\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} R(\tau^n) \nabla logP_{\theta}(a_n^t|s_n^t) \end{align} \]
这样,我们需要最大化的期望就可以写作最小化的Loss函数形式,如下所示:
\[ \begin{align} Loss=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} R(\tau^n)logP_{\theta}(a_n^t|s_n^t) \end{align} \]
我们继续对上式中的\(R(\tau^n)\)进行拆解。
最寻常的Return就是从当前时间点到结束的Reward的累计和,如下所示:
\[R(\tau^n) = \sum_{t=1}^{T_n}r_t^n\]
通过上面的方法计算Return存在以下缺点:
- 当前时刻所作出的动作应该只会影响之后的reward,和之前步骤的reward应该无关。---》改进方法:\(R(\tau^n)\)只计算当前时刻之后的累积。
- 一个动作对接下来的几步影响是大的,但对接下来很远步骤的影响力应该减小。---》改进方法:\(R(\tau^n)\)引入衰减因子\(\gamma\),越远影响越小。
则上式优化为:
\[R(\tau^n) = \sum_{t^{\prime}=t}^{T_n} \gamma^{t^{\prime}-t}r_{t^{\prime}}^n=R_t^n\]
这样,我们的Loss函数可以写成:
\[ \begin{align} Loss=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} R_t^nlogP_{\theta}(a_n^t|s_n^t) \end{align} \]
到这里,我们就可以根据上面的Loss函数训练我们的强化学习模型了。其中\(T_n\)可视做LLM中句子的长度,\(N\)可视做batch的大小。
但是,仅通过上述Loss函数做优化,还存在许多缺点,我们继续一步一步添加PPO算法中的优化对上述Loss函数进行改进。
PPO
奖励减去baseline
在好的局势下,无论做什么动作都能得到正的Reward;而在坏的局势下,无论做什么动作都会得到负的Reward。如下图所示:
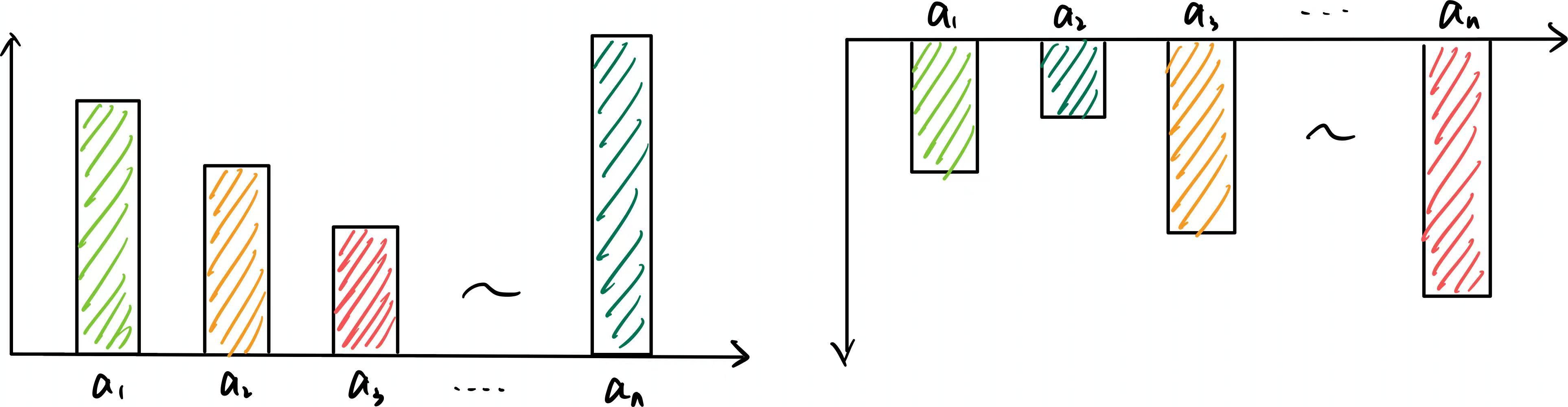
这是不合适的,我们需要的是当前这个动作相对于其他动作的优势,即只要这个动作相对于其他的动作好的话,则给他正向的奖励,反之给负向的奖励。所以这就需要我们对奖励减去一个baseline。
\[ \begin{align} Loss=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} (R_t^n - B(s_n^t))logP_{\theta}(a_n^t|s_n^t) \end{align} \]
我们把\(R_t^n -
B(s_n^t)\)称为一个动作对其他动作的优势。
这样,无论在好的局势下还是坏的局势下,我们得到的奖励都是有正有负的,更利于强化学习的训练,如下图所示:
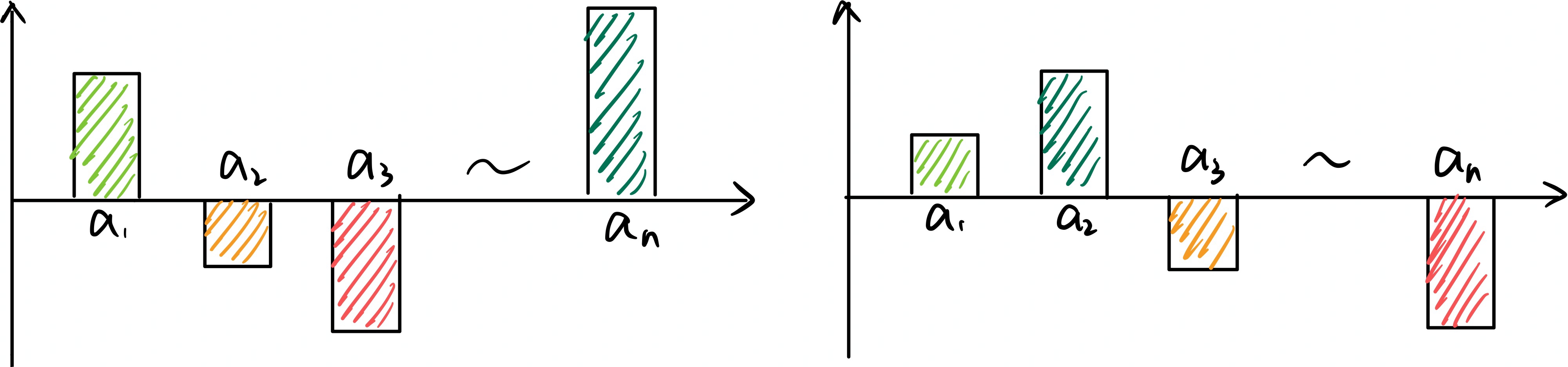
引入优势函数
计算Return的式子:
\[ \begin{align} Return = R_t^n - B(s_n^t) \\ R_t^n = \sum_{t^{\prime}=t}^{T_n} \gamma^{t^{\prime}-t}r_{t^{\prime}}^n \end{align} \]
可以看到,\(R_t^n\)是一次随机采样,方差很大,只有采样次数足够多的时候才会比较准确。那么是不是可以不通过采样,而是通过一个神经网络来估计\(R_t^n - B(s_n^t)\)这个优势呢?PPO算法在这里就引入了优势函数网络,通过一个神经网络直接预测相对优势。
几个概念:
- Action-Value Function(动作价值函数): \(Q_{\phi}(s, a)\),在状态s下,做出动作a的期望回报。
- State-Value Function(状态价值函数):\(V_{\phi}(s)\),在状态s下的期望回报。
- Advantage Function(优势函数):\(A_{\phi}(s, a)=Q_{\phi}(s, a)-V_{\phi}(s)\),在状态s下,做出动作a,相比于其他动作能带来多少优势。
这样,Loss函数就可以更新为:
\[ \begin{align} Loss &= -\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} (R_t^n - B(s_n^t))logP_{\theta}(a_n^t|s_n^t) \\ &\Rightarrow -\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} A_{\phi}(s_n^t, a_n^t)logP_{\theta}(a_n^t|s_n^t) \end{align} \]
下面进一步拆解优势函数\(A_{\phi}(s, a)=Q_{\phi}(s, a)-V_{\phi}(s)\)。
首先\(Q_{\phi}(s_t, a)\)可以理解为当前状态\(s_t\)下,作出动作\(a\)的期望回报。同时,它也等效于当前状态\(s_t\)下,作出动作\(a\)的奖励加上下一个状态\(s_{t+1}\)的期望回报,写作下式:
\[Q_{\phi}(s_t, a) = r_t + \gamma * V_{\phi}(s_{t+1})\]
然后,把\(Q_{\phi}(s_t, a)\)代入优势函数可以得到:
\[A_{\phi}(s_t, a)=r_t + \gamma * V_{\phi}(s_{t+1})-V_{\phi}(s_t)\]
这样我们就可以通过一个预测状态价值\(V_{\phi}(s)\)的神经网络去计算得到优势函数,如下图所示:
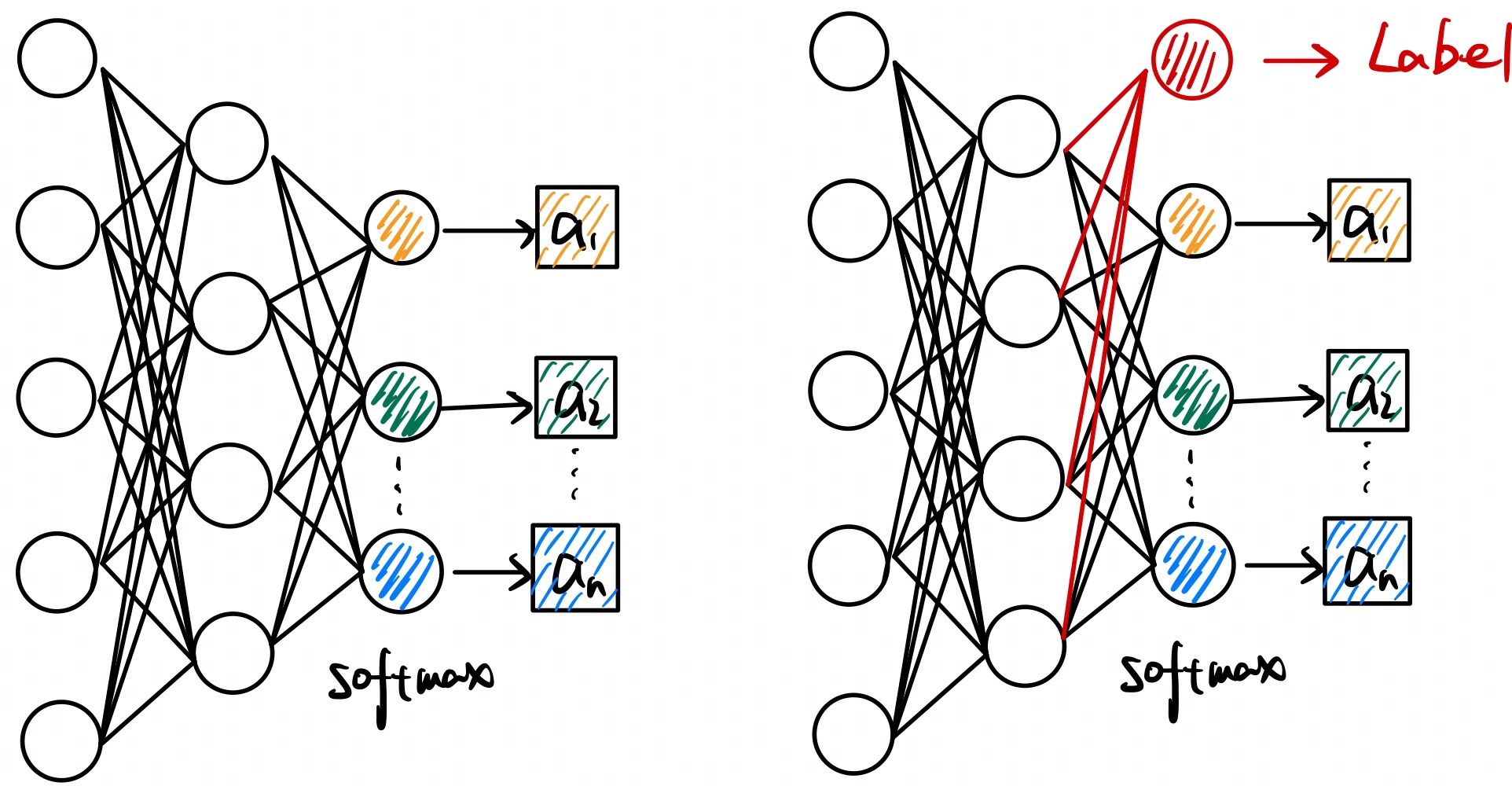
其中,左图为我们需要训练的模型\(\theta\),其输出为在当前状态下每个动作的输出概率。右图为状态价值网络\(\phi\),其输出为当前状态下的期望回报。
状态价值网络可以和要训练的模型\(\theta\)结构相同,只是最后一层不再是动作空间Action
Space的大小,而是输出单一的一个值,来代表当前状态的价值。
预测状态价值的网络的训练Label可表示为\(Label =
R_t^n = \sum_{t^{\prime}=t}^{T_n}
\gamma^{t^{\prime}-t}r_{t^{\prime}}^n\),用价值网络来拟合该Return值即可。
GAE
由于\(V_{\phi}\)的值都是通过神经网络估计的,所以\(A_{\phi}\)会存在偏差,GAE的目的就是在偏差和方差之前取得均衡。
对于状态价值\(V_{\phi}(s_t)\)的计算,我们可以直接在当前时间直接通过神经网络预测,即直接得到:
\[V_{\phi}(s_t)\]
我们也可以先现在当前时间随机采样一个动作\(a\),得到奖励\(r_t\),然后再通过神经网络预测下一个状态的价值,即得到:
\[V_{\phi}(s_t) \approx r_t + \gamma * V_{\phi}(s_{t+1})\]
更进一步,我们可以采样两步,然后再通过神经网络预测,即得到
\[V_{\phi}(s_t) \approx r_t + \gamma * r_{t+1} + \gamma^2 * V_{\phi}(s_{t+2})\]
以此类推,我们可以向后一直采样,得到采样多个步骤的优势函数如下:
\[ \begin{align} A^1_{\phi}(s_t, a) &= r_t + \gamma * V_{\phi}(s_{t+1}) - V_{\phi}(s_t) \\ A^2_{\phi}(s_t, a) &= r_t + \gamma * r_{t+1} + \gamma^2 * V_{\phi}(s_{t+2}) - V_{\phi}(s_t) \\ ... \\ A^{\infty}_{\phi}(s_t, a) &= \sum_{b=0}^{\infty}\gamma^br_{t+b} - V_{\phi}(s_t) \end{align} \]
定义中间变量:
\[ \begin{align} \delta_t^V &= r_t + \gamma * V_{\phi}(s_{t+1}) - V_{\phi}(s_t) \\ \delta_{t+1}^V &= r_{t+1} + \gamma * V_{\phi}(s_{t+2}) - V_{\phi}(s_{t+1}) \\ \delta_{t+2}^V &= ... \end{align} \]
采样多个步骤的优势函数可简化为:
\[ \begin{align} A^1_{\phi}(s_t, a) &= \delta_t^V \\ A^2_{\phi}(s_t, a) &= \delta_t^V + \gamma \delta_{t+1}^V \\ ... \\ A^{\infty}_{\phi}(s_t, a) &= \sum_{b=0}^{\infty}\gamma^b \delta_{t+b}^V \end{align} \]
那么在优势函数计算的时候,应该使用采样了几步的优势函数呢,GAE的做法是全都要:
\[ \begin{align} A_{\phi}^{GAE}&=(1 - \lambda)(A_{\phi}^1 + \lambda A_{\phi}^2 + \lambda^2A_{\phi}^3 + ...) \\ &=\sum_{b=0}^{\infty}(\gamma \lambda)^b\delta_{t+b}^V \end{align} \]
可以看到:
- 当\(\lambda=0\)时,\(A_{\phi}^{GAE}=r_t + \gamma * V_{\phi}(s_{t+1}) -
V_{\phi}(s_t)\),此时\(V_{\phi}\)的比重较大,偏差大,方差小,称为差分形式。
- 当\(\lambda=1\)时,\(A_{\phi}^{GAE}=\sum_{b=0}^{\infty}\gamma^br_{t+b} - V_{\phi}(s_t)\),此时\(V_{\phi}\)的比重较小,偏差小,方差大,称为蒙特卡洛形式。
我们可以通过调节\(\lambda\)的大小来对偏差和方差做一个权衡。
这样,经过PPO算法中GAE步骤的改进,我们的损失函数变为如下形式:
\[ \begin{align} Loss &= -\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} A_{\phi}(s_n^t, a_n^t)logP_{\theta}(a_n^t|s_n^t) \\ &\Rightarrow -\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} A_{\phi}^{GAE}(s_n^t, a_n^t)logP_{\theta}(a_n^t|s_n^t) \end{align} \]
其中\(A_{\phi}^{GAE}\)通过如下方式计算:
\[ \begin{align} A_{\phi}^{GAE}(s_t, a)=\sum_{b=0}^{\infty}(\gamma \lambda)^b\delta_{t+b}^V \\ \delta_t^V = r_t + \gamma * V_{\phi}(s_{t+1}) - V_{\phi}(s_t) \end{align} \]
On-Policy变为Off-Policy

什么是On-Policy模型和Off-Policy模型?以上图为例子:
- 被直接表扬的同学就是On-Policy模型,他直接从老师的表扬和批评中进行学习:当老师表扬其某个动作\(a_i\)时,其增大当前状态下该动作的概率;当老师批评其某个动作\(a_i\)时,则减小当前状态下该动作的概率。
- 身旁的同学就是Off-Policy模型,其通过On-Policy模型间接的从老师的表扬和批评中进行学习:当其看到老师表扬On-Policy模型的某个动作\(a_i\)时,其增大当前状态下该动作的概率;当其看到老师批评On-Policy模型的某个动作\(a_i\)时,其减小当前状态下该动作的概率。
On-Policy网络存在训练效率太低的问题,如下图所示:

即如果通过On-Policy策略去教一个学生,我们需要先看他有哪些地方做的好/不好,然后对其进行表扬/批评,等他改进完成后,再继续观察他有哪些地方做的好/不好。这样采集数据就会很慢。 所以PPO算法这里引入了Off-Policy策略,将采集数据和训练模型这两个步骤解偶,从而加快训练效率。
重要性采样公式推导:
\[ \begin{align} E(f(x))_{x \sim p(x)} &= \sum_xf(x)*p(x) \approx \frac{1}{N} \sum_{n=1}^{N}{f(x)}_{x \sim p(x)} \\ &= \sum_xf(x) * p(x) \frac{q(x)}{q(x)} \\ &= \sum_xf(x) * \frac{p(x)}{q(x)} * q(x) \\ &= E(f(x) \frac{p(x)}{q(x)})_{x \sim q(x)} \\ &\approx \frac{1}{N} \sum_{n=1}^N {f(x) \frac{p(x)}{q(x)}}_{x \sim q(x)} \end{align} \]
将重要性采样公式应用到之前的Loss函数中得到:
\[ \begin{align} \nabla Loss&=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} A_{\phi}^{GAE}(s_n^t, a_n^t) \nabla logP_{\theta}(a_n^t|s_n^t) \\ &=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} A_{\phi}^{GAE}(s_n^t, a_n^t) \frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)} \nabla logP_{\theta}(a_n^t|s_n^t) \end{align} \]
其中\(\theta^{\prime}\)就是直接受到老师批评/表扬的学生,\(\theta\)就是旁边的同学,\(\theta^{\prime}\)的优势函数\(A_{\phi}^{GAE}(s_n^t,
a_n^t)\)就是老师对On-Policy模型的批评/表扬。
而\(\frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)}\)则是Off-Policy模型相对于On-Policy模型对\(A_{\phi}^{GAE}(s_n^t,
a_n^t)\)应该放大或缩小的程度。
如:老师批评On-Policy模型玩手机,On-Policy模型要做出改进。而Off-Policy模型玩手机的概率是On-Policy模型的两倍,则应该做出两倍的改进。
通过数学技巧\(\nabla logf(x)=\frac{\nabla f(x)}{f(x)}\)继续优化上面的式子:
\[ \begin{align} \nabla Loss&=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} A_{\phi}^{GAE}(s_n^t, a_n^t) \nabla logP_{\theta}(a_n^t|s_n^t) \\ &=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} A_{\phi}^{GAE}(s_n^t, a_n^t) \frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)} \nabla logP_{\theta}(a_n^t|s_n^t) \\ &=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} A_{\phi}^{GAE}(s_n^t, a_n^t) \frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)} \frac{\nabla P_{\theta}(a_n^t|s_n^t)}{P_{\theta}(a_n^t|s_n^t)} \\ &=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} A_{\phi}^{GAE}(s_n^t, a_n^t) \frac{\nabla P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)} \end{align} \]
这样,我们就得到了PPO算法Loss函数的进一步表现形式:
\[ \begin{align} Loss&=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} A_{\phi}^{GAE}(s_n^t, a_n^t) \frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)} \end{align} \]
其中:
- \(\theta^{\prime}\)为参考的网络,也称为Ref网络,我们用它来进行数据采样,并用该数据计算优势函数。
- \(\theta\)为我们真实要训练的网络,我们只需计算它做出某个动作的概率,除以参考网络的概率,从而调整优势函数的程度,并进一步训练网络。
可以看到,数据采集和我们要训练的网络是区分开的,这样我们就解决了On-Policy网络训练效率太低的问题。
加入KL散度
上面的情况有一点限制,即要求On-Policy模型和Off-Policy模型不要相差太远。不然Off-Policy模型很难学到有用的经验和教训。
例如,班上总是上课玩手机的同学今天没有玩手机了,老师表扬了他;但这样的行为对于从来不玩手机的学生来说没有意义,因为其本来就不玩手机。
同样,如果某个差生今天考试交了白卷,老师批评了他,但这样的批评对好学生来说同样没有意义,因为其不会交白卷。
所以PPO算法加入了KL散度来约束On-Policy模型和Off-Policy模型不要相差太远,如下所示:
\[ \begin{align} Loss_{ppo}&=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} A_{\phi}^{GAE}(s_n^t, a_n^t) \frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)} + \beta KL(P_{\theta}, P_{\theta^{\prime}}) \end{align} \]
更进一步,PPO2中提出了截断来替代KL散度:
\[ \begin{align} Loss_{ppo2}&=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n} min(A_{\phi}^{GAE}(s_n^t, a_n^t) \frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)}, A_{\phi}^{GAE}(s_n^t, a_n^t)clip(\frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)}, 1 - \epsilon, 1 + \epsilon)) \end{align} \]
GRPO
PPO 与 GRPO 的对比分析
GRPO 首次在Pushing the Limits of Mathematical Reasoning in Open Language Models中提出,它在 PPO 的基础上引入了下面几个创新:
- 无需价值网络,显著降低了内存占用和计算开销
- 采用群组采样方法,实现更高效且稳定的优势估计
- 通过强化目标函数和奖励的惩罚机制,实现更保守的策略更新
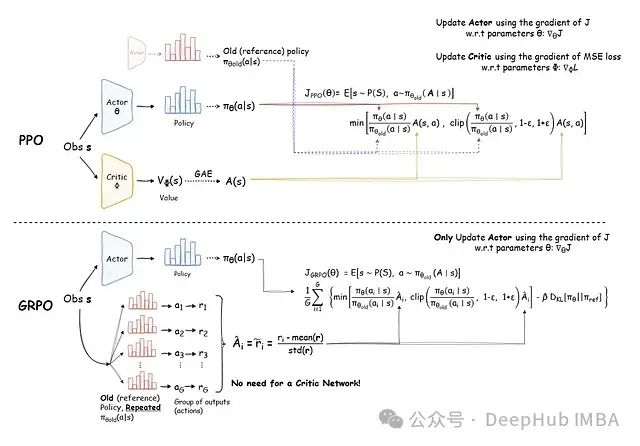
上图使用了https://avoid.overfit.cn/post/05d4b8fb001b4adeb4e050fb323cd21f这里的图,和本文符号存在一些区别,详细流程可参考下面的式子。
GRPO技术解析
GRPO优势函数估计流程如下:
- 对于LLM中的每个问题,使用\(\theta^{\prime}\)生成\(G\)个不同的输出序列。
- 计算每个输出序列的累积奖励,即\(R_{t,i}^n = \sum_{t^{\prime}=t}^{T_n} \gamma^{t^{\prime}-t}r_{t^{\prime},i},i=1,2,...,G\)。
- 奖励归一化,计算相对优势,使用归一化后的奖励作为优势函数的估计值。表现为\(A_{t,i}^n \approx \frac{R_{t, i}^n - mean(R_{t}^n)}{std(R_{t}^n)}\)。
- 在组内进行计算目标函数的平均值,\(\frac{1}{G} \sum_{i=1}^G min\left[A_{t,i}^n \frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)}, A_{t,i}^n clip(\frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)}, 1 - \epsilon, 1 + \epsilon)\right]\)。
这样,GRPO的Loss表现为:
\[Loss = -\frac{1}{N}\frac{1}{G}\frac{1}{T_n}\sum_{n=1}^{N}\sum_{i=1}^G\sum_{t=1}^{T_n} min\left[A_{t,i}^n \frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)}, A_{t,i}^n clip(\frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)}, 1 - \epsilon, 1 + \epsilon)\right]\]
更进一步GRPO论文中在上式中加入了KL散度的约束,最终Loss如下:
\[ \begin{align} Loss = -\frac{1}{N}\frac{1}{G}\frac{1}{T_n}\sum_{n=1}^{N}\sum_{i=1}^G\sum_{t=1}^{T_n} min \left\{\left[A_{t,i}^n \frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)}, A_{t,i}^n clip(\frac{P_{\theta}(a_n^t|s_n^t)}{P_{\theta^{\prime}}(a_n^t|s_n^t)}, 1 - \epsilon, 1 + \epsilon) \right] - \beta D_{KL}[(P_{\theta}, P_{\theta^{\prime}})] \right\} \\ D_{KL}[(P_{\theta}, P_{\theta^{\prime}})] = \frac{P_{\theta^{\prime}}(a_n^t|s_n^t)}{P_{\theta}(a_n^t|s_n^t)} - log\frac{P_{\theta^{\prime}}(a_n^t|s_n^t)}{P_{\theta}(a_n^t|s_n^t)} - 1 \end{align} \]
该目标函数的特点:
- 同时在群组和序列长度维度上进行平均
- 使用裁剪机制确保策略更新的保守性
- 引入 KL 散度估计作为惩罚项,防止策略与参考模型产生过大偏离