优化器(optimizer)介绍

发表于 更新于 分类于 ， 阅读次数： Disqus： 本文字数： 1.6k 阅读时长 ≈ 6 分钟

介绍SGD、SGDM、Adagrad、RMSProp、Adam等优化器算法

SGD

SGD全称Stochastic Gradient Descent，随机梯度下降，1847年提出。每次选择一个mini-batch，而不是全部样本，使用梯度下降来更新模型参数。它解决了随机小批量样本的问题，但仍然有自适应学习率、容易卡在梯度较小点等问题。

SGD的计算公式为：

\[\theta^t = \theta^{t-1} - \eta g^{t-1}\]

其中，\(\eta\)为学习率，\(g^{t-1}\)为\(t-1\)时刻的梯度。

SGD计算过程如下图所示：

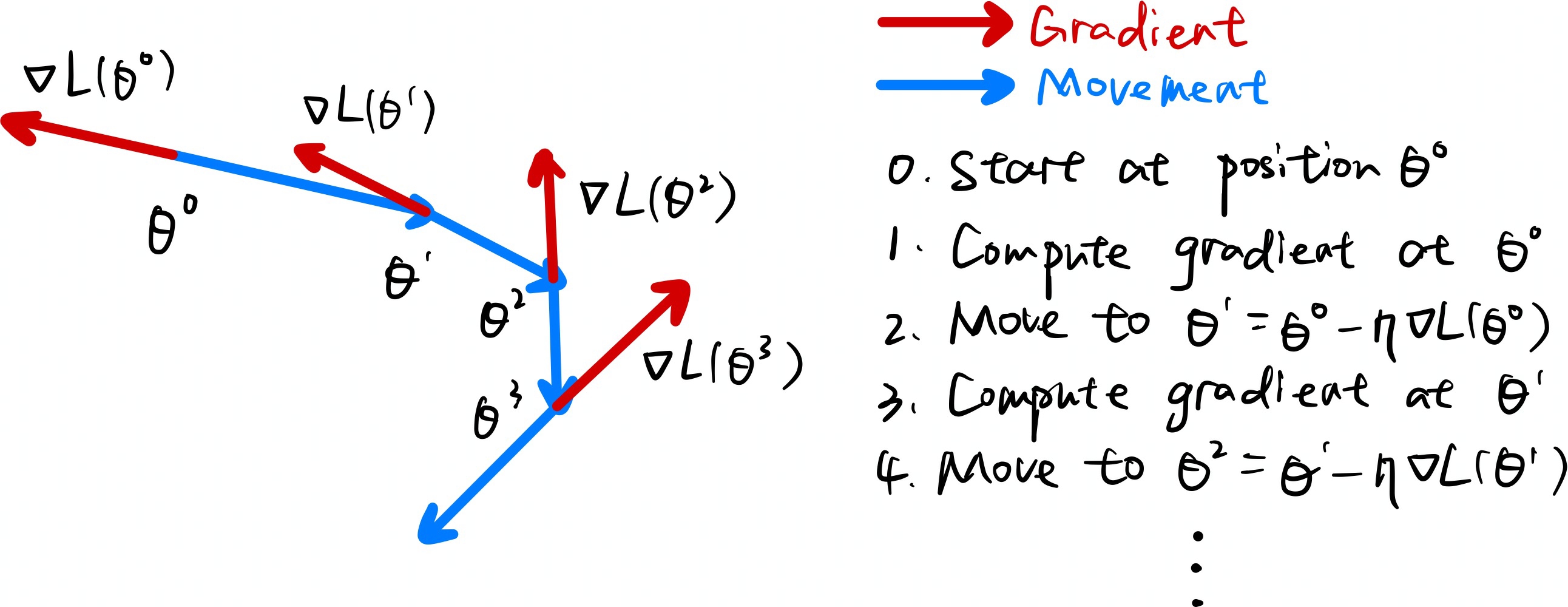
SGDM

SGDM即为SGD with momentum，它在SGD的基础上加入了动量机制，1986年提出。

SGDM的计算公式为：

\[ \begin{align} \theta^t = \theta^{t-1} - \eta m_t \\ m_t = \lambda m_{t-1} + g_{t-1} \end{align} \]

SGDM计算过程如下图所示：

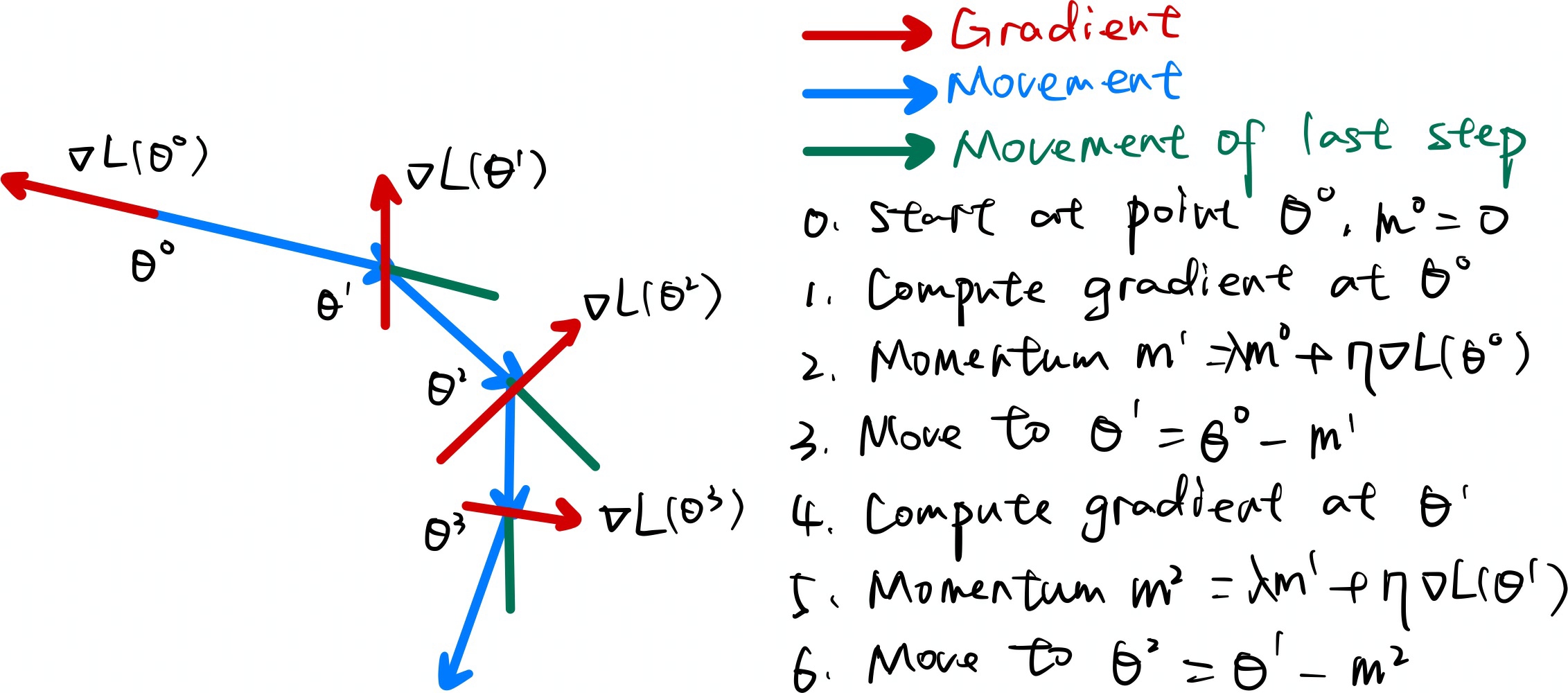
可以看到，此时\(\theta^{t-1}\)减去的不再是当前的梯度，而是前\(t-1\)次迭代的梯度的加权累积。其中\(\lambda\)为衰减权重，越远的迭代权重越小。
从而我们可以发现，SGDM相比于SGD的差别就在于，参数更新时，不仅仅减去了当前迭代的梯度，还减去了前\(t-1\)迭代的梯度的加权和。加入动量后，参数更新就可以保持之前更新趋势，而不会卡在当前梯度较小的点了。如下图所示：

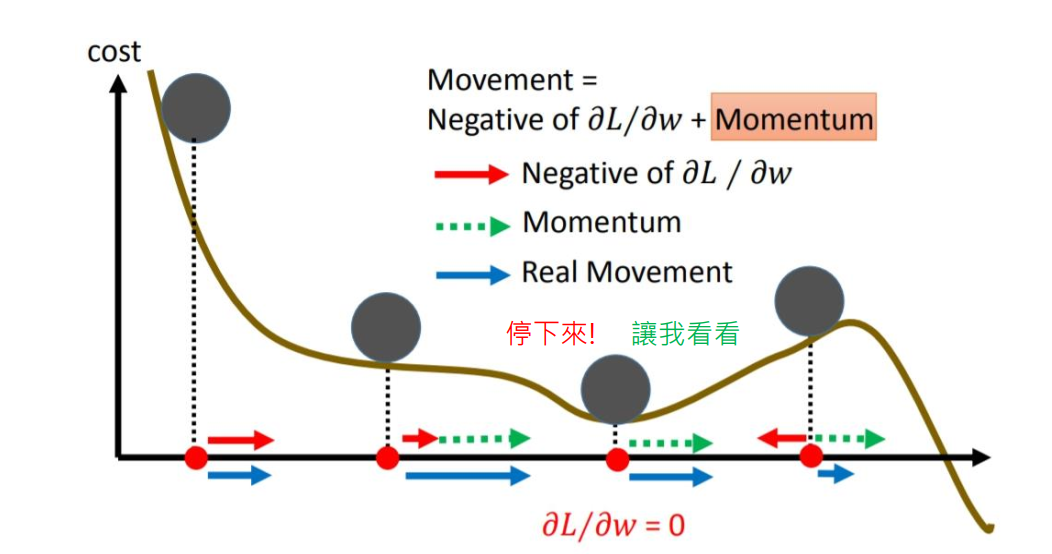
美中不足的是，SGDM没有考虑对学习率进行自适应更新，故学习率的选择很关键。

Adagrad

Adagrad在2011年提出，它利用迭代次数和累积梯度，对学习率进行自动衰减，从而使得刚开始迭代时，学习率较大，可以快速收敛。而后来则逐渐减小，精调参数，使得模型可以稳定找到最优点。

Adagrad的计算公式为：

\[ \begin{align} \theta^t = \theta^{t-1} - \frac{\eta}{\sqrt{\sum \limits_{t=0}^{t-1}(g_i^2)}}g_{t-1} \end{align} \]

Adagrad与SGD的区别在于学习率除以前\(t-1\)迭代的梯度的平方和,故称为自适应梯度下降。

但Adagrad有个致命问题，就是没有考虑迭代衰减。极端情况，如果刚开始的梯度特别大，而后面的比较小，则学习率基本不会变化了，也就谈不上自适应学习率了。这个问题在RMSProp中得到了修正。

RMSProp

RMSProp的计算公式为：

\[ \begin{align} \theta^t = \theta^{t-1} - \frac{\eta}{\sqrt{v_t}}g_{t-1} \\ v_t = \alpha v_{t-1} + (1 - \alpha)g_{t-1}^2 \end{align} \]

在RMSProp中，梯度累积不是简单的前\(t-1\)次迭代梯度的平方和了，而是加入了衰减因子α，越远的迭代梯度权重越小。

Adam

Adam在2015年提出，是SGDM和RMSProp的结合。

回顾上面说的SGDM和RMSProp。

SGDM的计算公式：

\[ \begin{align} \theta^t &= \theta^{t-1} - \eta m_t \\ m_t &= \beta_1 m_{t-1} + (1-\beta_1)g_{t-1} \end{align} \]

RMSProp的计算公式：

\[ \begin{align} \theta^t &= \theta^{t-1} - \frac{\eta}{\sqrt{v_t}}g_{t-1} \\ v_t &= \beta_2 v_{t-1} + (1 - \beta_2)g_{t-1}^2 \end{align} \]

结合上面两式，则Adam的计算公式为：

\[ \begin{align} \theta^t &= \theta^{t-1} - \frac{\eta}{\sqrt{v_t}}m_t \\ m_t &= \beta_1 m_{t-1} + (1-\beta_1)g_{t-1} \\ v_t &= \beta_2 v_{t-1} + (1 - \beta_2)g_{t-1}^2 \end{align} \]

Adam在真实使用时还加入了de-biasing，如下所示：

\[ \begin{align} \theta^t &= \theta^{t-1} - \frac{\eta}{\sqrt{\hat{v_t} + \epsilon}}\hat{m_t} \\ \hat{m_t} &= \frac{m_t}{1-\beta_1^t} \\ \hat{v_t} &= \frac{v_t}{1-\beta_2^t} \\ m_t &= \beta_1 m_{t-1} + (1-\beta_1)g_{t-1} \\ v_t &= \beta_2 v_{t-1} + (1 - \beta_2)g_{t-1}^2 \end{align} \]

其中\(\beta_1\)取值一般为0.9，\(\beta_2\)取值一般为0.999，\(\epsilon\)取值一般为\(10^{-8}\)。

更进一步，AdamW引入了weight decay，计算过程如下所示：

Muon

Muon的计算过程为：

其中\(B_t\)即相当于之前的\(m_t\)，NewtonSchulz5为Newton-schulz矩阵迭代：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Pytorch code
def newtonschulz5(G, steps=5, eps=1e-7):
    assert G.ndim == 2
    a, b, c = (3.4445, -4.7750, 2.0315)
    X = G.bfloat16()
    X /= (X.norm() + eps)
    if G.size(0) > G.size(1):
        X = X.T
    for _ in range(steps):
        A = X @ X.T
        B = b * A + c * A @ A
        X = a * X + B @ X
    if G.size(0) > G.size(1):
        X = X.T
    return X

MuonClip

参考https://github.com/MoonshotAI/Kimi-K2/blob/main/tech_report.pdf

MuonClip在Kimi-K2中被使用。他们发现大模型训练存在MaxLogit爆炸现象，MaxLogit爆炸是指，\(S_{max}\)随着训练的推进一直往上涨，增长速度是线性甚至是超线性的，并且在相当长的时间内没有稳定的迹象。

\[S_{max} = \max \limits_{i,j} q_i k_j\]

因为：

\(|q_ik_j| \leq ||q_i|| ||k_j|| = ||x_iW_q|| ||x_jW_k|| \leq ||x_i|| ||x_j|| ||W_q|| ||W_k||\)

由于\(x\)通常会加RMSNorm，所以一般情况下\(||x_i||||x_j||\)是不会爆炸的，因此MaxLogit爆炸意味着谱范数\(||Wq||,||Wk||\)有往无穷大发展的风险，可能会导致训练崩溃。因此，保险起见应当尽量避免MaxLogit爆炸的出现。

MuonClip在Muon的基础上使用了QK-Clip，如下所示：

\[ \begin{align} if\ S_{max}^{(l)} > \tau \ and \ W \in \{W_q^{(l)}, W_k^{(l)}\}: \\ W_t \leftarrow W_t \times \sqrt{\tau / S_{max}^{(l)}} \end{align} \]

也就是说，在优化器更新之后，根据\(S_{max}^{(l)}\)的大小来决定是否对\(Q,K\)的权重进行裁剪，裁剪的幅度直接由\(S_{max}^{(l)}\)与阈值\(\tau\)的比例来决定，直接保证裁剪后的矩阵不再MaxLogit爆炸。

在实际使用中，MuonClip为了避免过度裁剪，对Attention的多个Head分别进行监控MaxLogit和QK-Clip，并且由于Kimi-K2使用了MLA，所以上述公式更新为：

\[ \begin{align} &if\ S_{max}^{(l,h)} > \tau: \\ &\qquad if\ W \in \{W_{qc}^{(l,h)}, W_{kc}^{(l,h)}\}: \\ &\qquad \qquad W_t \leftarrow W_t \times \sqrt{\tau / S_{max}^{(l,h)}} \\ &\qquad elif\ W \in \{W_{qr}^{(l,h)}\}: \\ &\qquad \qquad W_t \leftarrow W_t \times \tau / S_{max}^{(l,h)} \end{align} \]

MLA的\(Q,K\)有\(qr、qc、kr、kc\)四部分，其中\(kr\)是所有Head共享的。

不管哪种Attention变体都有多个Head，如果每一层Attention只监控一个MaxLogit指标，所有Head的Logit是放在一起取Max的，这导致QK-Clip是将所有Head一起Clip的。然而，实际上每层只有为数不多的Head会出现MaxLogit爆炸，如果所有Head按同一个比例来Clip，那么大部份Head都是被“无辜受累”的了，这就是过度裁剪的含义。