【文献阅读】Native Sparse Attention: Hardware-Aligned and Natively Trainable Sparse Attention
论文地址:
Native Sparse Attention(NSA)是DeepSeek-AI团队开发的框架,用以解决Transformer架构中注意力机制\(O(n^2)\)复杂度的问题。
参数的设定:
- 序列长度设定为N=32k,即32768,相当于一本短篇小说的长度
- 滑动窗口大小w=512
- 压缩块大小l=32
- 压缩块步长d=16
- 选择块大小l'=64
- 选择块数量n=16
注意,为了方便,下面所有的计算都忽略了MultiHead。
设计理念
NSA的核心设计哲学源于对人类阅读行为的深入观察。人类在处理长文档时并非对每个词语给予相等的注意力,而是采用分层的认知策略。这种策略可以概括为三个并行的注意力机制:专注于当前句子的本地上下文处理、回顾前文章节的全局摘要理解,以及对关键段落和重要信息的选择性关注。
NSA将这种认知模式转化为三个计算分支:
- Sliding Window:专注于当前句子的本地上下文
- Token Compression:提供全局摘要
- Token Selection:实现关键信息扫描
这三个分支的输出通过门控机制智能融合,形成完整的语义理解。
Sliding Window
滑动窗口分支旨在保留最近本地上下文中的细粒度信息,确保模型对当前位置附近的语义关系具有高精度的理解能力。
该分支将注意力计算限制在最近的\(w=512\)个键值对范围内,并在此局部窗口上执行标准的注意力计算。计算公式如下所示:
\[Output_{win}=Attention(q_t, K_{t-w:t}, V_{t-w:t})\]
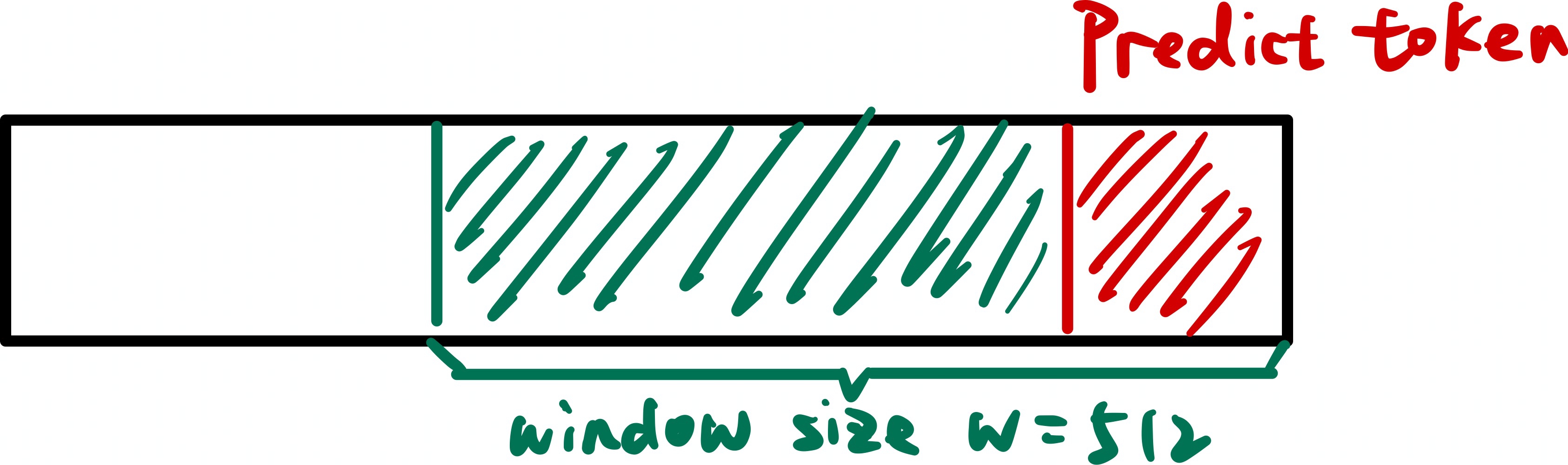
计算复杂度分析: 处理单个token的计算成本为\(O(w)\),这是一个与整体序列长度\(N\)无关的常数。整个序列的总计算成本为\(O(N*w)\),相比标准的\(O(N^2)\)复杂度实现了线性化的显著改进。
Token Compression
压缩分支负责快速高效地构建整个序列历史的粗粒度全局视图,这是理解文档整体结构和主题的关键步骤。
步骤1:从32768个token的原文生成2047个token的摘要
在序列上滑动大小为\(l=32\)的窗口,每次前进\(d=16\)个token,形成50%的重叠覆盖。这种重叠设计可以减轻块边界处的信息碎片化现象,确保生成的摘要具有良好的连续性。这样,长度为\(N=32768\)的序列就可以被分割为2047个块,这里的块被称为压缩块,如下图所示:

Token Compression生成的块的数量可以由公式\(floor(\frac{N-l}{d}) + 1\)计算得到。
其中\(N\)为序列长度,\(l\)为压缩块大小,\(d\)为压缩步长。
代入可得\(压缩块数量=floor(\frac{32768 -
32}{16}) + 1=2047\)。
通过上述步骤,原始的长度为32768的token序列被转换为包含2047个压缩块的表示,每个块由32个token组成。假设每个Attention
Head的维度\(d_k=128\),则矩阵形状可表示为[32, 128]。
论文指出,为保持向量的局部顺序信息,系统会向这些向量添加块内位置编码。
然后矩阵通过一个小型的MLP(论文中记为\(\varphi\),MLP通过多层线性变换和非线性激活函数,学习如何从32个输入token中提取和聚合最重要的语义信息),得到形状为[1, 128]的输出。如下图所示:
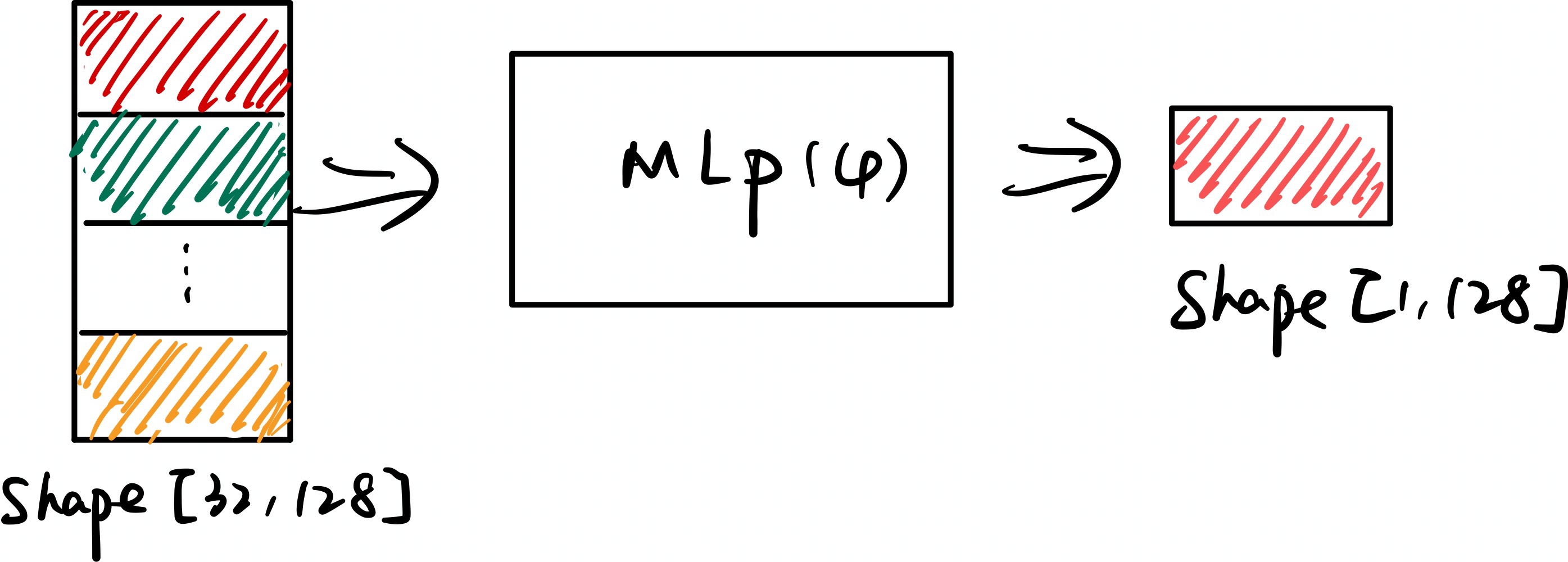
这一过程在所有2047个块上重复执行,最终生成形状为[2047, 128]的压缩键矩阵\(K_{cmp}\),同理可以得到压缩值矩阵\(V_{cmp}\)。
这样,注意力计算只需要在长度为2047的摘要上进行,而不需要对原始的N个token进行注意力计算,相当于序列长度由原来的32768缩减为2047。
步骤2:在摘要上进行注意力计算
接下来在\(q_t,\ K_{cmp},\ V_{cmp}\)上进行标准的注意力计算,如下式所示:
\[ \begin{align} p_{cmp}&=Softmax(q_t K_{cmp}^T) \\ Output_{cmp} &= p_{cmp}V_{cmp} \end{align} \]
其中,\(q_t \in R^{1 \times 128}\),\(K_{cmp} \in R^{2047 \times 128}\),\(V_{cmp} \in R^{2047 \times 128}\),注意力分数\(p_{cmp} \in R^{1 \times 2047}\),\(Output_{cmp} \in R^{1 \times 128}\)。
Token Selection
选择分支专注于捕获关键的长程细粒度依赖关系,通过将计算资源集中于文本中最相关的部分来实现这一目标。
Blockwise Selection & Importance Score Computation
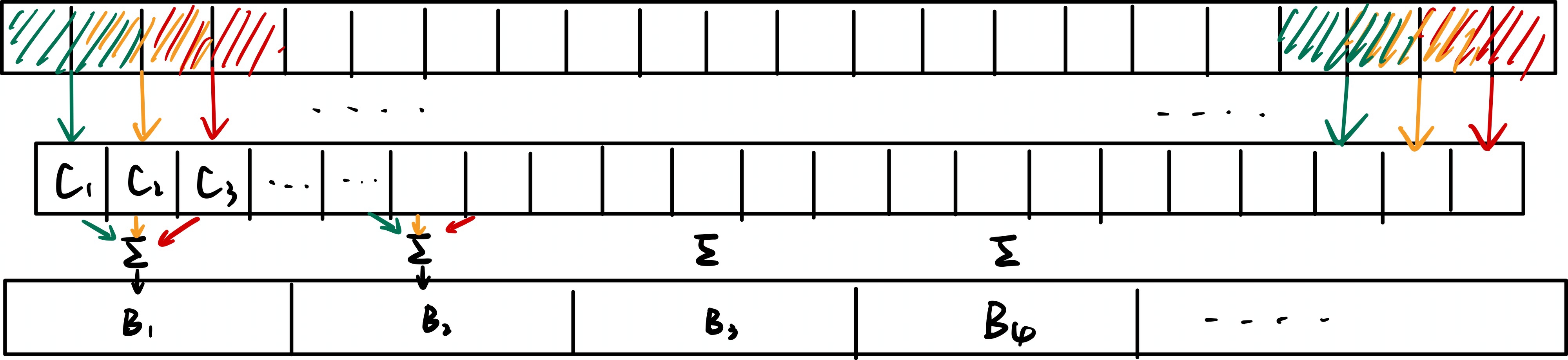
首先将原文分成512个块,每个块的大小为64(\(512 \times 64=32768\)),这里的块被称为选择块。对于选择块i,通过对与其空间有重叠的压缩块的\(p_{cmp}\)分数进行求和来计算选择块的重要性分数,计算方法如下:
\[p_t^{slc}[i] = \sum_{j \in overlapping\ blocks}p_t^{cmp}[j]\]
计算图示如下所示:
Top-𝑛 Block Selection
得到了每个选择块的分数之后,我们需要从中选出最具有潜力的块进行进一步详细的分析,论文中直接选取Top16个分数最高的选择块进行注意力计算。
每个选择块的大小为64个token,取Top16个选择块的位置索引\(I_t\),并选取原始键向量和值向量的对应向量组成\(K_{slc}\)和\(V_{cls}\)。然后进行注意力计算:
\[Output_{slc} = Attention(q_t, K_{slc}, V_{slc})\]
其中,\(q_t \in R^{1 \times 128}\),\(K_{slc} \in R^{16 \times 64 \times 128}\),\(V_{slc} \in R^{16 \times 64 \times 128}\),\(Output_{slc} \in R^{1 \times 128}\)。
门控输出融合机制
最后,我们来融合三个分支(\(Output_{win}、Output_{cmp}、Output_{slc}\))的输出结果。采用一个小型可学习的门控多层感知器,以\(q_t\)作为输入,为每个分支生成相应的"门控"分数。通过Sigmoid激活函数确保这些分数处于0到1的范围内,使其能够作为各分支输出的权重系数。如下所示:
对应公式如下:
\[ \begin{align} o_t &= \sum_{c \in \{win,cmp,slc\}}g_t^c Output_c \\ g_t &= MLP(q_t) \end{align} \]