FlashAttention算法

转载自https://zhuanlan.zhihu.com/p/1940732079726912160。

GPU构成

在学习计算机时，我们一般会将存储分为寄存器、内存、硬盘。它们的容量依次递增，读写速度依次递减。硬盘一般只负责存储数据，上面的数据不能做直接运算。内存存储了程序能直接「看到」的数据。使用高级编程语言时，内存是我们存储数据和对数据做运算的地方。但在最底层的运算实现中，程序实际上是先把数据从内存搬到寄存器上，再做运算，最后把数据搬回内存。只有在编写更底层的汇编语言时，我们才需要知道寄存器这一层。

当然，实际上在寄存器和内存之间还有缓存（cache）这一层，但这属于硬件上的实现细节，它在编程模型中是不可见的，硬件会自动处理缓存的逻辑。

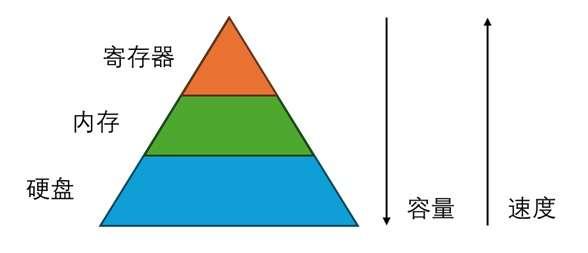
类似地，在 GPU 上，也有类似的存储模型。CPU 内存 (DRAM) 上的数据不能直接用 GPU 运算，必须要放到 GPU HBM 里，就像对 CPU 中硬盘和内存的关系一样。GPU HBM 就是我们常说的「显存」。使用高级语言（如 PyTorch）编写 GPU 程序时，我们可以认为数据全是在 HBM 上运算的。同样，在更底层，我们需要先把数据从 GPU HBM 读取到 GPU SRAM （类似于 CPU 中的寄存器）上，做运算，再把数据写回 GPU HBM。

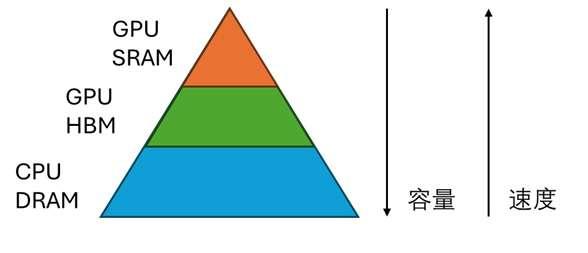
认识了存储模型后，我们来看 GPU 编程模型相比高级语言的编程模型有哪些变化。

在高级语言中，如果要把两个变量相加得到第三个变量，只需要编写如下代码。

c = a + b

而加入了「访存」这一概念后，我们需要在计算前后加入变量的读取和存储指令。此外，如果计算中产生了新的变量，需要为新变量新建空间。如下面的代码所示，a_mem, b_mem, 是在 GPU HBM 上的变量，我们用需要用 load 把它们读入到 SRAM 中，得到 SRAM 上的变量 a, b。之后，我们在 SRAM 上创建新变量 c, 并用它存储加法结果。最后把 c 写回 HBM 的 c_mem 里。

c_mem = new_hbm_memory()

a = a_mem.load()
b = b_mem.load()

c = new_sram_memory()
c = a + b

c_mem = c.store()

可以看出，为了实现一次加法，我们做了两次读取，一次存储，访存带来的时间开销不可忽略。

除此之外，这里为新变量创建空间的操作出现了两次：一次是在 HBM，一次是在 SRAM。上面这个例子比较简单，输入输出都只有一个变量，没有空间不足的问题。但一般来说，算子的输入都是很长的数组。我们默认 HBM 的存储空间一定足够，但 SRAM 的空间不一定足够。因此，我们需要用到「分块」操作，一块一块地把输入从 HBM 读入到 SRAM 并运算。

FlashAttention 的主要贡献就是减少了 Attention 的内存操作开销（读取、存储、新建空间）。

算子融合

通过上面的例子，我们发现，算上了访存后，哪怕是实现一个简单的加法都十分费劲。因此，大多数程序员都只会编写高级语言，并让编译器来自动补全访存的逻辑。比如对于 c=a+b 而言，编译器会自动生成两个读取指令，一个存储指令。

可是，编译器自动生成的 GPU 代码一定是最优的吗？这显然不是。考虑下面这个高级语言中的函数 add_more：

def add_more(a, b, c, d):
  a1 = a + b
  a2 = a + c
  a3 = a + d
  return a1, a2, a3

如果让编译器按照最直接的方式翻译这段高级语言，那么翻译出的 GPU 程序中会包含如下的指令（为只关注读写次数，我们不写变量在 HBM 上的名称，默认所有变量都在 SRAM 上，且忽略新建空间操作）：

load a, b
a1 = a + b
store a1

load a, c
a2 = a + c
store a2

load a, d
a3 = a + d
store a3

但仔细观察这些读写指令，我们会发现部分读写指令是多余的：a 只要被读取一次就行了。最优的程序应为：

load a, b, c, d
a1 = a + b
a2 = a + c
a3 = a + d
store a1, a2, a3

由于我们知道了 add_more 函数的某些特性，我们可以通过手写 GPU 程序，而不是让编译器死板地逐行翻译算子的方式，实现一个更高效的「大型算子」。这种做法被称为 「算子融合」(operator fusion)。由于 GPU 上的函数一般被称为 kernel，所以这种做法也会称为「核融合」(kernel fusion)。

并行编程

和使用高级语言编程相比，在进行 GPU 编程时，我们除了要考虑访存，还需要编写可以并行执行的程序。我们说 GPU 比 CPU 快，并不是因为 GPU 里的计算单元比 CPU 的高级，而是因为 GPU 里的计算单元更多。用一个常见的比喻，GPU 编程就像是把复杂的数学运算拆成简单的加减乘除，再交给许许多多的小学生来完成。作为 GPU 程序员，我们不仅要决定运算的过程，还需要像「小学老师」一样，知道如何把整个运算拆成若干个更简单、可并行执行的运算。

为了快速入门并行编程，我们先通过一个简单的例子来了解一般并行程序的写法，再通过一个反例认识怎样的运算是不能并行的。最后，我们会简要总结并行编程的设计方式。

考虑这样一个向量加法任务：假设向量数组 a, b, c 的长度都是 16，我们要在 4 个 GPU 计算单元上实现 c=a+b 的操作，应该怎么为每个计算单元编写程序呢？

最直观的想法肯定是把向量平均拆成四组，让每个计算单元计算 4 个分量的加法结果。这是因为如果任务分配不均匀，任务完成的总时间会取决于任务最多的那个计算单元，这个时间会比平均分更久。因此，我们可以为每个计算单元各自编写如下所示的程序。

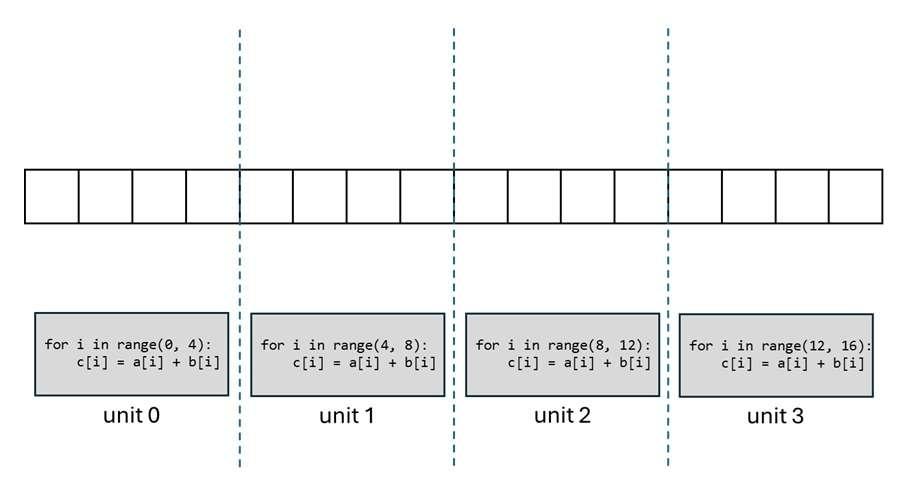
为每个计算单元单独写一段程序太累了，能不能只写一段程序，然后让所有计算单元都执行同一段程序呢？这当然可以，但还有一个小小的额外要求：由于现在所有计算单元共用一段程序，我们需要额外输入当前计算单元的 ID 来告知程序正在哪个计算单元上运行。得知了这个额外信息后，我们就可以自动算出当前计算单元应该处理的数据范围，写出下面的程序。

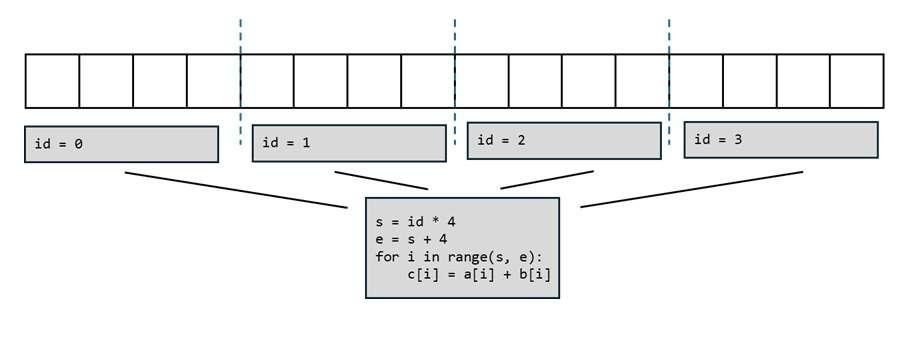
有了这段通用的程序，我们其实就可以实现任意长向量的加法运算。比如当向量的长度变成 32 时，我们可以分配 8 个计算单元来计算。可见，并行编程的目标就是写一段通用的程序，并根据计算单元的 ID 选取同样数量的数据做计算。

在上面的例子中，我们让每个计算单元都计算 4 个数据。实际情况中，应该给每个计算单元分配多少数据呢？一般来说，一个计算单元的并行计算器和存储空间都是有限的，应该尽可能用满它的计算资源。比如一个计算单元最多能并行算 4 个数据，且内存也只够存 4 个数据，那么我们就给它分配 4 个数据。

FlashAttention的计算优化

考虑attention计算：

\[Attn(A,B)=softmax(QK^{\top})V\]

算子融合

PyTorch 版 Attention 的代码如下所示。

光看 PyTorch 代码，我们还看不出哪里还有优化空间。因此，我们可以把访存操作加进去。假设一行 PyTorch 代码对应一个标准库里的 GPU 算子，要加入的 IO 操作如下。

这样，我们就能立刻发现一个可优化项：中间变量 s, p 前脚刚写入 HBM，后脚又被读回了 SRAM。如果能用算子融合技术，把整个 Attention 运算放到同一个 GPU 算子里，就能规避这些额外的访存操作。

并行编程

需要注意的是，如果中间变量不多，多读写两次并不会浪费多少时间。然而，此处的 s, p 是两个数据量很大的变量。这是因为在当今大模型的 Transformer 中，（多头注意力的）特征维度 D 一般只是 32, 64 这样比较小的数，而序列长度 SL 至少是\(10^4\)这个数量级。所以，形状为 [SL, SL] 的中间变量 s, p 比形状为 [SL, D] 的输入输出要大得多，它们的访存开销严重拖慢了普通 Attention 的速度。

现在，我们来考虑如何把 Attention 都在同一个 GPU 算子里实现。如前文所述，每个 GPU 程序描述了一个计算单元上的运算。而由于计算单元本身的 SRAM 存储是有限的，我们需要根据程序 ID，拆分数据，仅处理部分数据。这里，我们假设每个计算单元能存储量级为 D 的数据，但无法存储量级为 SL 的数据。

基于这一限制，我们来继续修改上面的程序。现在，我们不能一次读写形状为 [SL, D] 的数据了，该怎么拆分任务呢？在前文有关注意力运算的回顾中，我们知道，每个 query 之间的运算是独立的。因此，我们可以在上一份代码的基础上修改，只不过这一次我们只在一个并行程序里处理一个 query 和一个 output 的计算。

当然，除了 Q, O，我们也不能一次性读写全部 K, V 了。既然如此，我们只能使用循环，在每一步迭代里读一个 k 或 v。改写后的程序如下。

可是，程序中还有一处超出了内存限制：通过拆分运算，我们将中间变量 s, p 的形状从 [SL, SL] 降低到了 [SL]，但它们依然超过了内存限制。能否优化它们的内存占用呢？这一步优化，正是 FlashAttention 的核心贡献。

softmax 在 attention 中的实现如下。

拆分了 softmax 之后，我们立刻就能发现一个可优化项：变量 s[i] 被求了一次 exp 后就再也没用过了。既然如此，我们不必再用一个循环求 numerator，只需要求出了 q, k 的点乘 s 后，立刻求 numerator[i] = exp(s[i]) 即可。

类似地，我们也不用在另一个循环里对分母求和，一边算一边求和即可。

做完这些优化后，我们确实消除了 softmax 的部分冗余运算。然而，最关键的问题还是没有解决：中间变量 numerator, p 的长度依然是 SL，该怎么接着优化呢？

刚刚我们把 softmax 的部分操作和 q, k 点乘合并了。能否顺着这个思路，把剩余操作和 p, v 的乘法合并呢？

问题的瓶颈在 p 的分母上。如果不需要除以那个 softmax 的分母，就没那么多限制了。我们先尝试忽略除法那一行，看看代码能优化多少。这时，可以把后面的循环和前面的循环合并起来，得到下面的代码。

接着，我们来回头纠正输出。这个错误的 O 和之前正确的结果差了多少？其实就是少除以了一个 denominator。并且，修改了代码后，有关 denominator 的计算完全没变过。循环结束后，denominator 也就算出来了。所以，我们完全可以在循环结束后再除以分母。

改完代码后，我们发现，p 不用再算了，只剩最后一个长度为 SL 的变量了——numerator。仔细观察代码，现在我们每次只需要用到 numerator[i]，不需要重新访问整个 numerator 向量。既然如此，我们可以把 numerator 向量换成一个临时变量。

终于，这份程序成为了一段满足内存限制的可运行 GPU 程序。相比各个运算用独立算子表示的 PyTorch 版 Attention，这份高效 Attention 实现规避了形状为 [SL, SL] 的中间变量的读写开销，大大提升了运行效率。这版 Attention 就是一种简易的 FlashAttention。